使用Python求解带约束的最优化问题详解
更新时间:2020年02月11日 10:18:47 作者:深山里的小白羊
今天小编就为大家分享一篇使用Python求解带约束的最优化问题详解,具有很好的参考价值,希望对大家有所帮助。一起跟随小编过来看看吧
题目:

1. 利用拉格朗日乘子法
#导入sympy包,用于求导,方程组求解等等
from sympy import *
#设置变量
x1 = symbols("x1")
x2 = symbols("x2")
alpha = symbols("alpha")
beta = symbols("beta")
#构造拉格朗日等式
L = 10 - x1*x1 - x2*x2 + alpha * (x1*x1 - x2) + beta * (x1 + x2)
#求导,构造KKT条件
difyL_x1 = diff(L, x1) #对变量x1求导
difyL_x2 = diff(L, x2) #对变量x2求导
difyL_beta = diff(L, beta) #对乘子beta求导
dualCpt = alpha * (x1 * x1 - x2) #对偶互补条件
#求解KKT等式
aa = solve([difyL_x1, difyL_x2, difyL_beta, dualCpt], [x1, x2, alpha, beta])
#打印结果,还需验证alpha>=0和不等式约束<=0
for i in aa:
if i[2] >= 0:
if (i[0]**2 - i[1]) <= 0:
print(i)
结果:
(-1, 1, 4, 6) (0, 0, 0, 0)
2. scipy包里面的minimize函数求解
from scipy.optimize import minimize
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
#目标函数:
def func(args):
fun = lambda x: 10 - x[0]**2 - x[1]**2
return fun
#约束条件,包括等式约束和不等式约束
def con(args):
cons = ({'type': 'ineq', 'fun': lambda x: x[1]-x[0]**2},
{'type': 'eq', 'fun': lambda x: x[0]+x[1]})
return cons
#画三维模式图
def draw3D():
fig = plt.figure()
ax = Axes3D(fig)
x_arange = np.arange(-5.0, 5.0)
y_arange = np.arange(-5.0, 5.0)
X, Y = np.meshgrid(x_arange, y_arange)
Z1 = 10 - X**2 - Y**2
Z2 = Y - X**2
Z3 = X + Y
plt.xlabel('x')
plt.ylabel('y')
ax.plot_surface(X, Y, Z1, rstride=1, cstride=1, cmap='rainbow')
ax.plot_surface(X, Y, Z2, rstride=1, cstride=1, cmap='rainbow')
ax.plot_surface(X, Y, Z3, rstride=1, cstride=1, cmap='rainbow')
plt.show()
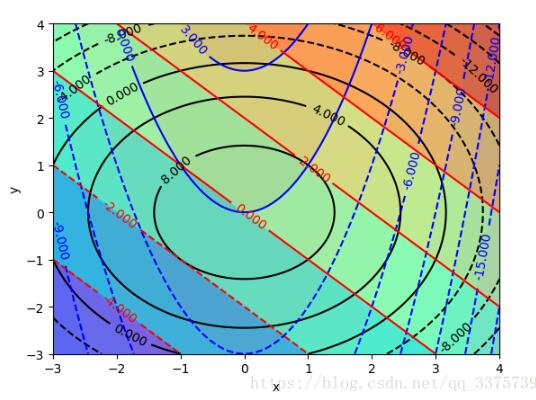
#画等高线图
def drawContour():
x_arange = np.linspace(-3.0, 4.0, 256)
y_arange = np.linspace(-3.0, 4.0, 256)
X, Y = np.meshgrid(x_arange, y_arange)
Z1 = 10 - X**2 - Y**2
Z2 = Y - X**2
Z3 = X + Y
plt.xlabel('x')
plt.ylabel('y')
plt.contourf(X, Y, Z1, 8, alpha=0.75, cmap='rainbow')
plt.contourf(X, Y, Z2, 8, alpha=0.75, cmap='rainbow')
plt.contourf(X, Y, Z3, 8, alpha=0.75, cmap='rainbow')
C1 = plt.contour(X, Y, Z1, 8, colors='black')
C2 = plt.contour(X, Y, Z2, 8, colors='blue')
C3 = plt.contour(X, Y, Z3, 8, colors='red')
plt.clabel(C1, inline=1, fontsize=10)
plt.clabel(C2, inline=1, fontsize=10)
plt.clabel(C3, inline=1, fontsize=10)
plt.show()
if __name__ == "__main__":
args = ()
args1 = ()
cons = con(args1)
x0 = np.array((1.0, 2.0)) #设置初始值,初始值的设置很重要,很容易收敛到另外的极值点中,建议多试几个值
#求解#
res = minimize(func(args), x0, method='SLSQP', constraints=cons)
#####
print(res.fun)
print(res.success)
print(res.x)
# draw3D()
drawContour()
结果:
7.99999990708696 True [-1.00000002 1.00000002]
以上这篇使用Python求解带约束的最优化问题详解就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持脚本之家。












最新评论