详解Python牛顿插值法
一、牛顿多项式
拉格朗日多项式的公式不具备递推性,每个多项式需要单独构造。但很多时候我们需要从若干个逼近多项式选择一个。这个时候我们就需要一个具有递推关系的方法来构造——牛顿多项式
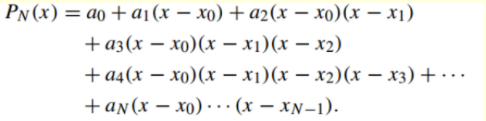
这里的的a0,a1…等可以通过逐一带入点的值来求得。但是当项数多起来时,会发现式子变得很大,这个时候我们便要引入差商的概念(利用差分思想)具体见式子能更好理解


这里在编程实现中我们可以推出相应的差商推导方程
d(k,0)=y(k)
d(k,j)=(d(k,j-1)-d(k-1,j-1)) / (x(k)-x(k-j))
二、例题
【问题描述】考虑[0,3]内的函数y=f(x)=cos(x)。利用多个(最多为6个)节点构造牛顿插值多项式。
【输入形式】在屏幕上依次输入在区间[0,3]内的一个值x*,构造插值多项式后求其P(x*)值,和多个节点的x坐标。
【输出形式】输出牛顿插值多项式系数向量,差商矩阵,P(x*)值(保留6位有效数字),和与真实值的绝对误差(使用科学计数法,保留小数点后6位有数字)。
【样例1输入】
0.8
0 0.5 1
【样例1输出】
-0.429726
-0.0299721
1
1 0 0
0.877583 -0.244835 0
0.540302 -0.674561 -0.429726
0.700998
4.291237e-03
【样例1说明】
输入:x为0.8,3个节点为(k, cos(k)),其中k = 0, 0.5, 1。
输出:
牛顿插值多项式系数向量,表示P2(x)=-0.429726x^2 - 0.0299721x + 1;
3行3列的差商矩阵;
当x为0.8时,P2(0.8)值为0.700998
与真实值的绝对误差为:4.291237*10^(-3)
【评分标准】根据输入得到的输出准确
三、ACcode:
C++(后面还有python代码)
/*
* @Author: csc
* @Date: 2021-04-30 08:52:45
* @LastEditTime: 2021-04-30 11:57:46
* @LastEditors: Please set LastEditors
* @Description: In User Settings Edit
* @FilePath: \code_formal\course\cal\newton_quo.cpp
*/
#include <bits/stdc++.h>
#define pr printf
#define sc scanf
#define for0(i, n) for (i = 0; i < n; i++)
#define for1n(i, n) for (i = 1; i <= n; i++)
#define forab(i, a, b) for (i = a; i <= b; i++)
#define forba(i, a, b) for (i = b; i >= a; i--)
#define pb push_back
#define eb emplace_back
#define fi first
#define se second
#define int long long
#define pii pair<int, int>
#define vi vector<int>
#define vii vector<vector<int>>
#define vt3 vector<tuple<int, int, int>>
#define mem(ara, n) memset(ara, n, sizeof(ara))
#define memb(ara) memset(ara, false, sizeof(ara))
#define all(x) (x).begin(), (x).end()
#define sq(x) ((x) * (x))
#define sz(x) x.size()
const int N = 2e5 + 100;
const int mod = 1e9 + 7;
namespace often
{
inline void input(int &res)
{
char c = getchar();
res = 0;
int f = 1;
while (!isdigit(c))
{
f ^= c == '-';
c = getchar();
}
while (isdigit(c))
{
res = (res << 3) + (res << 1) + (c ^ 48);
c = getchar();
}
res = f ? res : -res;
}
inline int qpow(int a, int b)
{
int ans = 1, base = a;
while (b)
{
if (b & 1)
ans = (ans * base % mod + mod) % mod;
base = (base * base % mod + mod) % mod;
b >>= 1;
}
return ans;
}
int fact(int n)
{
int res = 1;
for (int i = 1; i <= n; i++)
res = res * 1ll * i % mod;
return res;
}
int C(int n, int k)
{
return fact(n) * 1ll * qpow(fact(k), mod - 2) % mod * 1ll * qpow(fact(n - k), mod - 2) % mod;
}
int exgcd(int a, int b, int &x, int &y)
{
if (b == 0)
{
x = 1, y = 0;
return a;
}
int res = exgcd(b, a % b, x, y);
int t = y;
y = x - (a / b) * y;
x = t;
return res;
}
int invmod(int a, int mod)
{
int x, y;
exgcd(a, mod, x, y);
x %= mod;
if (x < 0)
x += mod;
return x;
}
}
using namespace often;
using namespace std;
int n;
signed main()
{
auto polymul = [&](vector<double> &v, double er) {
v.emplace_back(0);
vector<double> _ = v;
int m = sz(v);
for (int i = 1; i < m; i++)
v[i] += er * _[i - 1];
};
auto polyval = [&](vector<double> const &c, double const &_x) -> double {
double res = 0.0;
int m = sz(c);
for (int ii = 0; ii < m; ii++)
res += c[ii] * pow(_x, (double)(m - ii - 1));
return res;
};
int __ = 1;
//input(_);
while (__--)
{
double _x, temp;
cin >> _x;
vector<double> x, y;
while (cin >> temp)
x.emplace_back(temp), y.emplace_back(cos(temp));
n = x.size();
vector<vector<double>> a(n, vector<double>(n));
int i, j;
for0(i, n) a[i][0] = y[i];
forab(j, 1, n - 1) forab(i, j, n - 1) a[i][j] = (a[i][j - 1] - a[i - 1][j - 1]) / (x[i] - x[i - j]);
vector<double> v;
v.emplace_back(a[n - 1][n - 1]);
forba(i, 0, n - 2)
{
polymul(v, -x[i]);
int l = sz(v);
v[l - 1] += a[i][i];
}
for0(i, n)
pr("%g\n", v[i]);
for0(i, n)
{
for0(j, n)
pr("%g ", a[i][j]);
puts("");
}
double _y = polyval(v, _x);
pr("%g\n", _y);
pr("%.6e",fabs(_y-cos(_x)));
}
return 0;
}
python代码
'''
Author: csc
Date: 2021-04-29 23:00:57
LastEditTime: 2021-04-30 09:58:07
LastEditors: Please set LastEditors
Description: In User Settings Edit
FilePath: \code_py\newton_.py
'''
import numpy as np
def difference_quotient(x, y):
n = len(x)
a = np.zeros([n, n], dtype=float)
for i in range(n):
a[i][0] = y[i]
for j in range(1, n):
for i in range(j, n):
a[i][j] = (a[i][j-1]-a[i-1][j-1])/(x[i]-x[i-j])
return a
def newton(x, y, _x):
a = difference_quotient(x, y)
n = len(x)
s = a[n-1][n-1]
j = n-2
while j >= 0:
s = np.polyadd(np.polymul(s, np.poly1d(
[x[j]], True)), np.poly1d([a[j][j]]))
j -= 1
for i in range(n):
print('%g' % s[n-1-i])
for i in range(n):
for j in range(n):
print('%g' % a[i][j], end=' ')
print()
_y = np.polyval(s, _x)
print('%g' % _y)
# re_err
real_y = np.cos(_x)
err = abs(_y-real_y)
print('%.6e' % err)
def main():
_x = float(input())
x = list(map(float, input().split()))
y = np.cos(x)
newton(x, y, _x)
if __name__ == '__main__':
main()
到此这篇关于详解Python牛顿插值法的文章就介绍到这了,更多相关Python牛顿插值法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!












最新评论