C语言如何实现一些算法或者函数你知道吗
更新时间:2022年03月01日 15:31:44 作者:cy Hunter
这篇文章主要为大家详细介绍了C语言实现一些算法或者函数,文中示例代码介绍的非常详细,具有一定的参考价值,感兴趣的小伙伴们可以参考一下,希望能够给你带来帮助
1.递归二分搜索
#include<bits/stdc++.h>
using namespace std;
int a[100];
int pos = -1;
void binarysearch(int l, int r, int x){
if(l > r)return;
else{
int mid = (l+r)/2;
if(x == a[mid]) {
pos = mid;
return;
}
if(x < a[mid]) return binarysearch(l, mid-1, x);
else return binarysearch(mid+1, r, x);
}
}
int main(){
int n;
cin>>n; //输入元素个数
for(int i=0; i<n; i++)cin>>a[i];
sort(a, a+n);
binarysearch(0, n-1, 5);//二分搜索
cout<<pos;//输出找到的位置下标
return 0;
}
结果示例
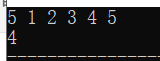
2.递归归并排序
3.Ackerman函数
#include<bits/stdc++.h>
using namespace std;
long Ackerman(long n, long m){
if(n >= 0 && m >= 0){
if(n == 1 && m == 0)return 2;
if(n == 0 && m >= 0)return 1;
if(n >= 2 && m == 0)return n+2;
if(n >= 1 && m >= 1)return Ackerman(Ackerman(n-1, m), m-1);
}
}
int main(){
long n, m;
cin>>n>>m;
cout<<Ackerman(n, m);
return 0;
}
结果示例
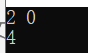
4.Fibonacci数列
#include<bits/stdc++.h>
using namespace std;
int fibonacci(int n){
if(n == 1)return 1;
else if(n == 2)return 1;
else return fibonacci(n-1)+fibonacci(n-2);
}
int main(){
int n;
cin>>n;//返回斐波那契数列第几项
cout<<fibonacci(n);
return 0;
}
结果示例
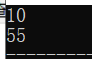
5.递归求排列
#include<bits/stdc++.h>
using namespace std;
int a[20], b[20];//a[]为排列的盒子,b[]为判断元素是否放过的数组
int n;
void perm(int k){//k表示开始放第k个数
if(k == n+1){//当k>n时说明第k个数已经放好,已经一组排列完毕
for(int i=1; i<=n; i++){
cout<<a[i]<<" ";
}
cout<<endl;
}
else{
for(int i=1; i<=n; i++){//1-n个数各自放入盒子a[]中
if(b[i] == 0){//初始化b[]都为0,为0说明这个数没放过
a[k] = i;//第k个数放入i
b[i] = 1;//i放了因此后面不能再放了
perm(k+1);//放第二个数。
b[i] = 0;//虽然第一次排列放了,但是第二次排列还需要用到。
}
}
}
}
int main(){
cin>>n;//排列数个数
perm(1);//从放第一个数开始排列
return 0;
}
示例结果
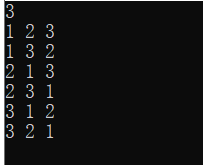
6.求最大公约数
#include<bits/stdc++.h>
using namespace std;
int gcd(int a, int b){
return b==0?a:gcd(b, b%a);
}
int main(){
int a, b;
cin>>a>>b;
cout<<gcd(a,b);
}
示例结果
7.偶位数的大整数乘法
#include<bits/stdc++.h>
using namespace std;
long mul(long x, long y, long n){
if(x == 0 || y == 0)return 0;
else if(n == 1)return x * y;
else{
long A = (long)x / pow(10, (long)(n/2));
long B = x - A * pow(10, n/2);
long C = (long)y / pow(10, (long)(n/2));
long D = y - C * pow(10, n/2);
long AC = mul(A, C, n/2);
long BD = mul(B, D, n/2);
long A_BD_C = mul((A - B),(D - C), n/2);
return AC * pow(10, n) + (A_BD_C + AC + BD)* pow(10, (long)(n/2)) + BD;
}
}
int main(){
long a, b, n, sign;
if((a<0 && b>0) || (a>0 && b<0))sign = -1;
else sign = 1;
cin>>a>>b>>n;
cout<<mul(a, b, n) * sign;
}
结果示例
总结
本篇文章就到这里了,希望能够给你带来帮助,也希望您能够多多关注脚本之家的更多内容!












最新评论