基于Pytorch的神经网络之Regression的实现
更新时间：2022年03月15日 10:15:49 作者：ZDDWLIG
本文主要介绍了基于Pytorch的神经网络之Regression的实现，文中通过示例代码介绍的非常详细，具有一定的参考价值，感兴趣的小伙伴们可以参考一下
1.引言
我们之前已经介绍了神经网络的基本知识，神经网络的主要作用就是预测与分类，现在让我们来搭建第一个用于拟合回归的神经网络吧。
2.神经网络搭建
2.1 准备工作
要搭建拟合神经网络并绘图我们需要使用python的几个库。
import torch import torch.nn.functional as F import matplotlib.pyplot as plt x = torch.unsqueeze(torch.linspace(-5, 5, 100), dim=1) y = x.pow(3) + 0.2 * torch.rand(x.size())
既然是拟合，我们当然需要一些数据啦，我选取了在区间 内的100个等间距点，并将它们排列成三次函数的图像。
2.2 搭建网络
我们定义一个类，继承了封装在torch中的一个模块，我们先分别确定输入层、隐藏层、输出层的神经元数目，继承父类后再使用torch中的.nn.Linear()函数进行输入层到隐藏层的线性变换，隐藏层也进行线性变换后传入输出层predict，接下来定义前向传播的函数forward()，使用relu()作为激活函数，最后输出predict()结果即可。
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(n_feature, n_hidden)
self.predict = torch.nn.Linear(n_hidden, n_output)
def forward(self, x):
x = F.relu(self.hidden(x))
return self.predict(x)
net = Net(1, 20, 1)
print(net)
optimizer = torch.optim.Adam(net.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()网络的框架搭建完了，然后我们传入三层对应的神经元数目再定义优化器，这里我选取了Adam而随机梯度下降(SGD)，因为它是SGD的优化版本，效果在大部分情况下比SGD好，我们要传入这个神经网络的参数(parameters)，并定义学习率(learning rate)，学习率通常选取小于1的数，需要凭借经验并不断调试。最后我们选取均方差法(MSE)来计算损失(loss)。
2.3 训练网络
接下来我们要对我们搭建好的神经网络进行训练，我训练了2000轮(epoch)，先更新结果prediction再计算损失，接着清零梯度，然后根据loss反向传播(backward)，最后进行优化，找出最优的拟合曲线。
for t in range(2000):
prediction = net(x)
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()3.效果
使用如下绘图的代码展示效果。
for t in range(2000):
prediction = net(x)
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if t % 5 == 0:
plt.cla()
plt.scatter(x.data.numpy(), y.data.numpy(), s=10)
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=2)
plt.text(2, -100, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 10, 'color': 'red'})
plt.pause(0.1)
plt.ioff()
plt.show()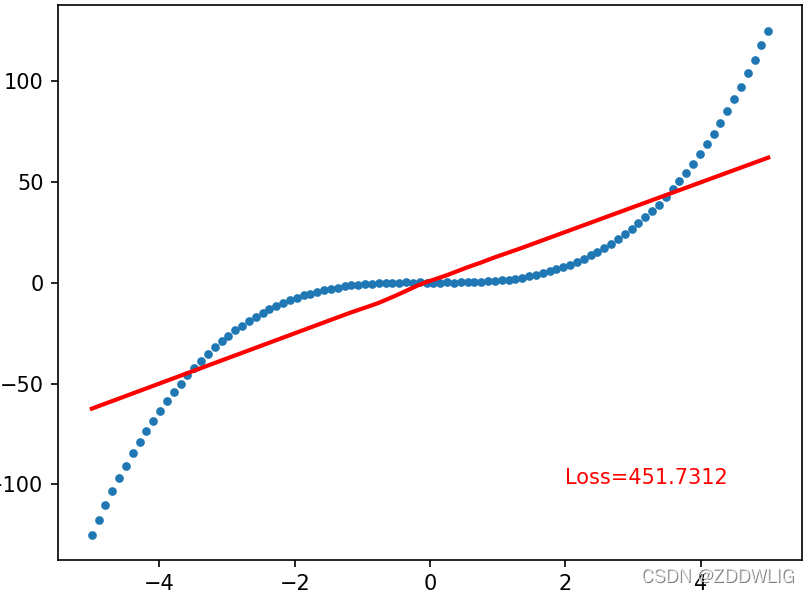
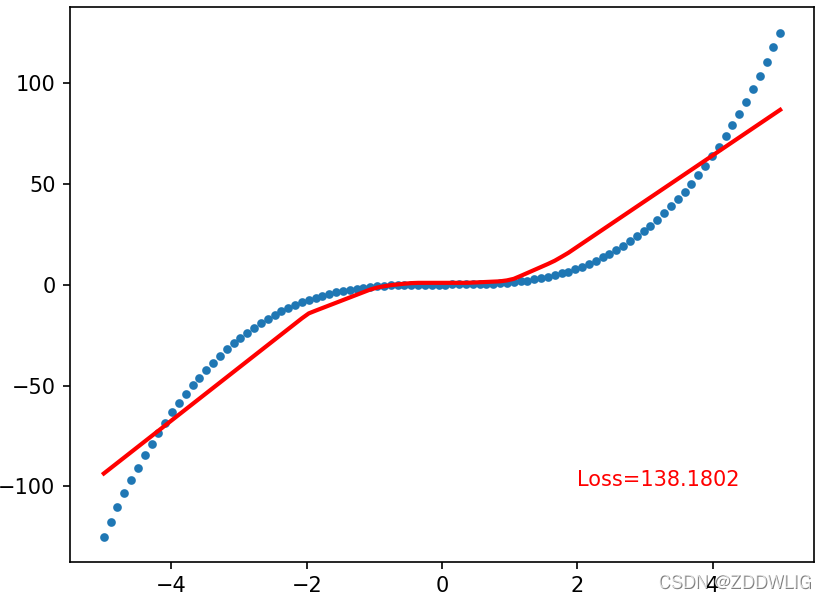
最后的结果：
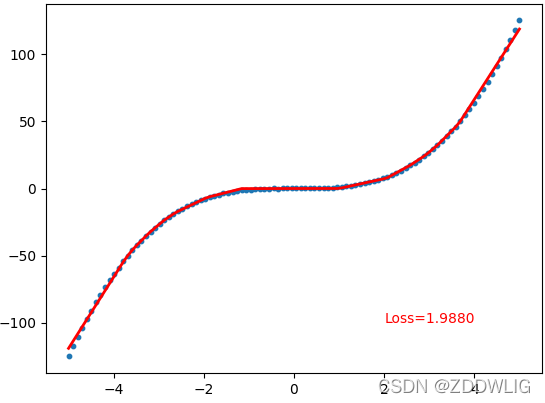
4. 完整代码
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-5, 5, 100), dim=1)
y = x.pow(3) + 0.2 * torch.rand(x.size())
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(n_feature, n_hidden)
self.predict = torch.nn.Linear(n_hidden, n_output)
def forward(self, x):
x = F.relu(self.hidden(x))
return self.predict(x)
net = Net(1, 20, 1)
print(net)
optimizer = torch.optim.Adam(net.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()
plt.ion()
for t in range(2000):
prediction = net(x)
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if t % 5 == 0:
plt.cla()
plt.scatter(x.data.numpy(), y.data.numpy(), s=10)
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=2)
plt.text(2, -100, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 10, 'color': 'red'})
plt.pause(0.1)
plt.ioff()
plt.show()到此这篇关于基于Pytorch的神经网络之Regression的实现的文章就介绍到这了,更多相关 Pytorch Regression内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！
您可能感兴趣的文章:
相关文章
本篇文章主要介绍了Python3安装Scrapy的方法步骤，小编觉得挺不错的，现在分享给大家，也给大家做个参考。一起跟随小编过来看看吧2017-11-11
这篇文章主要介绍了python使用pycharm环境调用opencv库，小编觉得挺不错的，现在分享给大家，也给大家做个参考。一起跟随小编过来看看吧2018-02-02
在现代数据驱动的世界中,生成清晰、有用的报表对于业务决策至关重要,Python作为一门强大的编程语言,提供了丰富的库和工具,使得报表自动化变得轻而易举,本文将详细介绍如何利用Python从数据处理到可视化,实现报表自动化的全过程2024-01-01
LyScript插件中提供了三种基本的堆栈操作方法，其中push_stack用于入栈，pop_stack用于出栈，peek_stac可用于检查指定堆栈位置处的内存参数。所以本文将利用这一特性实现对内存堆栈扫描，感兴趣的可以了解一下2022-08-08
这篇文章主要介绍了python 一篇文章搞懂装饰器所有用法，文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值，需要的朋友们下面随着小编来一起学习学习吧2021-10-10
这篇文章主要介绍了python获取本机mac地址和ip地址的方法,涉及Python获取系统相关信息的技巧,需要的朋友可以参考下2015-04-04
python中用shutil.move移动文件或目录的方法实例
在python操作中大家对os,shutil,sys,等通用库一定不陌生,下面这篇文章主要给大家介绍了关于python中用shutil.move移动文件或目录的相关资料,需要的朋友可以参考下2022-12-12
这篇文章主要介绍了python中的sort方法,需要的朋友可以参考下2014-07-07
从matplotlib的角度来说,绘图风格也算是图像类型的一部分,所以这篇文章小编想带大家了解一下Python中matplotlib的绘图风格,有需要的可以参考下2023-09-09
这篇文章主要介绍了Pycharm+Python工程,引用子模块的实现，具有很好的参考价值，希望对大家有所帮助。一起跟随小编过来看看吧2020-03-03
最新评论