C语言数据结构之堆排序的优化算法

在浏览本篇博文的小伙伴可先浅看一下上篇堆和堆排序的思想：

戳这里可跳转上篇文~~

1.堆排序优化算法

要堆堆排序算法进行优化我们首先要明白之前我们所写的堆排序有什么可以优化的地方或者说哪里写的不够好？

void HeapSort(int* a, int size)
{
	//小堆
	HP hp;
	HeapInit(&hp);
	//O(N*logN)
	for (int i = 0; i < size; ++i)
	{
		HeapPush(&hp, a[i]);
	}
	size_t j = 0;
	//O(N*logN)
	while (!HeapEmpty(&hp))
	{
		a[j] = HeapTop(&hp);
		j++;
		HeapPop(&hp);
	}
	HeapDestory(&hp);
}

这是我们之前写的堆排序，我们能够发现，如果我们要实现堆排序的前提是我们要写一堆。那这想想都很麻烦，我们都知道排序算法那么多，我们何必选择这种算法呢？

其次我们再来分析一下建堆的时间复杂度：

1.1建堆的时间复杂度

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明 ( 时间复杂度本来看的就是近似值，多几个节点不影响最终结果) ：

因为我们要进行优化建堆，在这里分析一下向下调整建堆和向上调整建堆的时间复杂度。

1.1.1 向下调整建堆：O(N)

过程分析如下：

因此向下调整建堆的时间复杂度为O(n)。

1.1.2 向上调整建堆：O(N*logN)

过程分析如下：

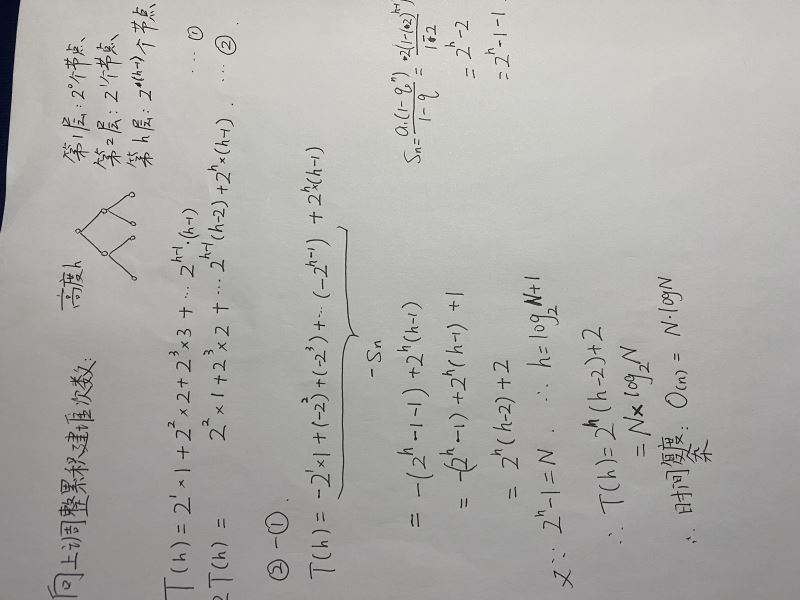
 因此向上调整建堆的时间复杂度为O(N*logN)。

1.2堆排序的复杂度

1.2.1原堆排序的时间复杂度

我们来看原堆排序的代码中使用了向上调整建堆，因此原排序的时间复杂度为O(N*logN)

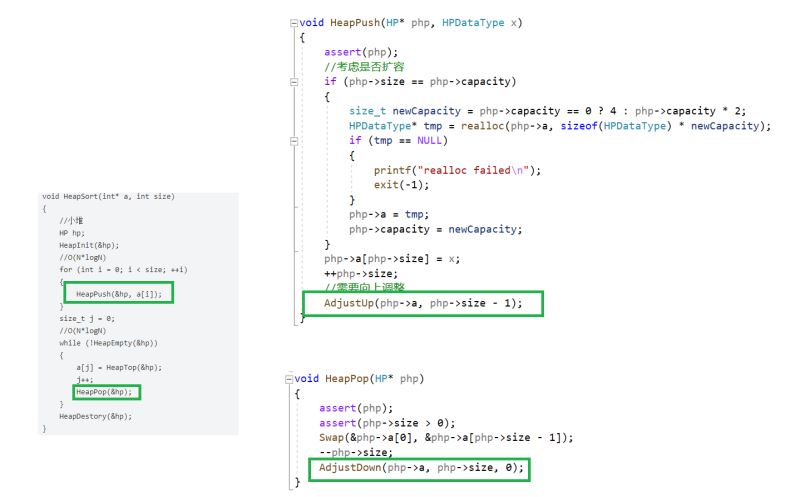
1.2.2原堆排序的空间复杂度

因为我们要建立一个堆，我们实现堆是使用数组实现，因此假设有要排序元素个数为N，空间复杂度为O(N)。

1.3堆排序优化算法的复杂度

堆排序的优化算法主要是对空间复杂度进行优化。由于我们之前建堆都要开辟新的数组，因此我们是否可以在原数组上直接建堆，无需再开辟新的空间建堆呢？答案当然是可以的。以下使用的正是在原数组上直接建堆。

1.3.1 堆排序优化算法的时间复杂度

由于使用堆排序，我们要利用堆的特点，每次取堆顶的元素。因此每次取完数据后都要对堆进行调整。再次我们有向上调整和向下调整两种算法，我们需要对这两种算法分别分析选出一个 更优的调整算法。

1.3.1.1向上调整--建堆 O(N*logN)

由于我们是对原数组之间建堆，因此我们如果要是用向上调整，在刚刚我们所分析的建堆的时间复杂度是O(N*logN)。

实现代码：

	向上调整--建堆  O(N*logN)
	int n = 1;
	while (n<size)
	{
		AdjustUp(a, n++);
	}

1.3.1.2向下调整-建堆 O(N)

由于向下调整的前提条件是左子树和右子树都已经是一个堆，但是一个数组并不能保证是一个堆，那么我们不能直接对数组使用向下调整。因此我们需要将节点的左子树右子树变成堆再进行向下调整。因此我们可以我们可以倒着来。

过程：

1、叶子节点不要调，因为一个节点可以看成堆。因此我们从倒数的第一个非叶子节点开始调整。如果找到倒数第一个非叶子节点。那就是用最后一个节点找他的父节点就是最后一个非叶子节点。

parent = (child-1)/2。我们用size计算：child = size -1。因此parent = (size-1-1)/2。我们一直向上找就可以将数组变成一个堆。因此向下调整建堆的复杂度为O(N)。分析如上：

	//向下调整--建堆  O(N)
	for (int i = (size - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, size, i);
	}

1.3.2 堆排序优化算法的空间复杂度

由于我们是在原数组上进行遍历因此没有开辟新的空间。因此空间复杂度为O(1)。

1.4堆排序实现逻辑

如果升序建小堆，最小的数已经在堆顶,剩下的数关系打乱,需要重新建堆,建堆最好也要O(N)，再选出次小的,不断建堆选数,如果这样,还不如直接遍历选数！！因此升序要建大堆！！利用删除的思想来玩。

过程：

1、把第一个数和最后一个数交换，由于是大堆，堆顶的数据一定是最大的数据。和最后一个数交换后，最大的数据就到了最后一个。

2、再对前N-1个数进行向下调整建立新的大堆，次大的数放在了堆顶，我们再让堆顶的元素和最后一个元素交换（这个最后一个不是数组的最后一个，是堆中的最后一个，使用end进行控制）。

3、当end到0的时候，说明已经排完了。

	//升序要建大堆,
	size_t end = size - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}

1.5堆排序实现代码

void HeapSort(int* a, int size)
{
	//向下调整--建堆  O(N)
	for (int i = (size - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, size, i);
	}
 
	//如果升序建小堆,最小的数已经在堆顶,剩下的数关系打乱,需要重新建堆,建堆最好也要O(N)
	//再选出次小的,不断建堆选数,如果这样,还不如直接遍历选数！！
 
	//升序要建大堆,
	size_t end = size - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
 
int main()
{
	int a[] = { 4,2,1,3,5,7,9,8,6};
	HeapSort(a,sizeof(a)/sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
	{
		printf("%d ", a[i]);
	}
  
	return 0;
}

1.6演示结果

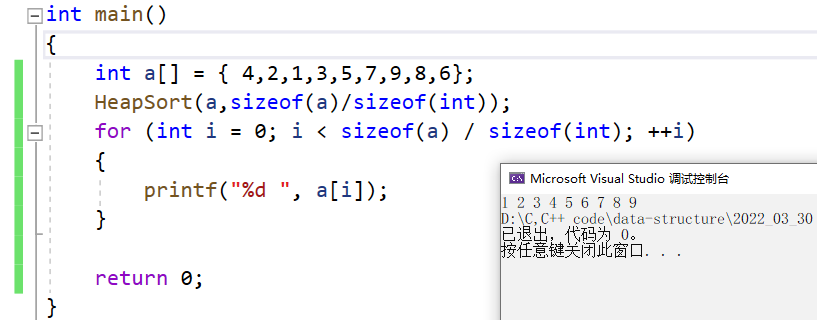
总结

到此这篇关于C语言数据结构之堆排序优化算法的文章就介绍到这了,更多相关C语言堆排序优化算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！

最新评论