Java实现拓扑排序的示例代码
铺垫
有向图:我们这节要讲的算法涉及到有向图,所以我先把有向图的一些概念说一下,文章后面就不做解释啦。首先有向图节点与节点之间是用带箭头的线连接起来的。节点有出度和入度的概念,连线尾部指向的节点出度加1,连线头部,也就是箭头指向的节点入度加1。看下面这个例子,A的入度为0,出度为2,B的入度为1,出度为1,C的入度为1,出度为1,D的入度为2,出度为0。
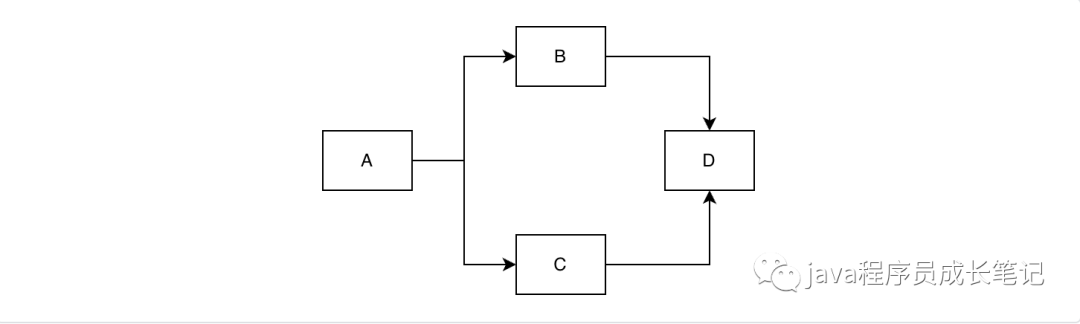
邻接表:邻接表是存储图结构的一种有效方式,如下图所示,左边节点数组存储图中所有节点,右侧邻接表存储节点的相邻节点。

简介
这篇文章我们要讲的是拓扑排序,这是一个针对有向无环图的算法,主要是为了解决前驱后继的关系,即我们在完成当前事项的时候需要先完成什么事项,其实这在我们流程控制里面用的挺多的。看下面这个图,我们需要先完成A事项,然后才能去完成B,C事项,B,C事项的属于并列的,没有先后顺序,但是对于D事项需要在B,C事项完成之后才能进行。而拓扑排序能够帮助我们找到这个完成事项的合理顺序,同时我们看上面这个例子,A事项完成之后,B,C事项是没有先后顺序的,不管是先完成B还是C都符合条件,所以拓扑排序的顺序序列不是完全一定的。
工作过程
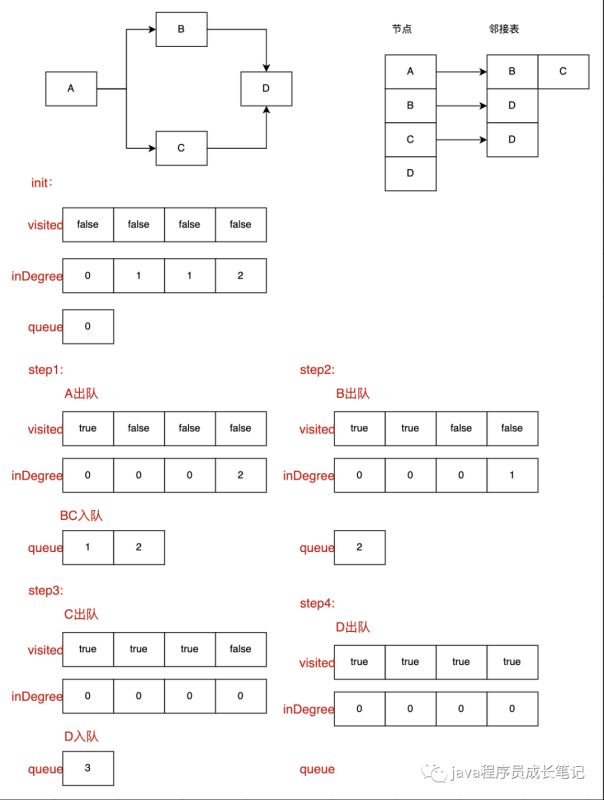
首先拓扑排序对应操作的是一个有向无环图。无环图,则肯定存在至少一个结点入度为0。在当前情况下,我们需要查找入度为0的节点进行操作,入度为0,表示当前节点没有前驱节点,或者前驱节点已经处理,可以直接操作。操作完毕之后,将当前节点的后继节点入度全部减1,再次查找入度节点为0的节点进行操作,此后就是一个递归过程,不断处理当前情况下入度为0的节点,直至所有节点处理完毕。
数据结构
有向图结构如下,其中node存储当前图中包含的所有节点,adj存储对应下标节点的邻接点。初始化图时候,我们需要初始化图中节点个数,存储节点的数组以及节点对应邻接数组。同时提供一个addEdge方法,用于在两个节点直接加边,其实就是将后继节点放入前驱节点的邻接表中。
public static class Graph{
/**
* 节点个数
*/
private Integer nodeSize;
/**
* 节点
*/
private char[] node;
/**
* 邻接表
*/
private LinkedList[] adj;
public Graph(char[] node) {
this.nodeSize = node.length;
this.node = node;
this.adj = new LinkedList[nodeSize];
for (int i = 0 ; i < adj.length ; i++) {
adj[i] = new LinkedList();
}
}
/**
* 在节点之间加边,前驱节点指向后继节点
* @param front 前驱节点所在下标
* @param end 后继节点所在下标
*/
public void addEdge(int front, int end) {
adj[front].add(end);
}
}拓扑排序
拓扑排序首先初始化了两个临时数组,一个队列,一个inDegree数组存储对应下标节点的入度,因为每次访问的节点需要前驱节点已经完成,即入度为0,有了这个数组我们就可以比较快速的找到这些节点;另一个是visited数组,标志当前节点是否已经访问过,防止多次访问;一个nodes队列则保存在目前情况下所有入度为0的节点。(注意,为了存取方便,我们都是存储的节点下标 step1:初始化inDegree数组,visited数组; step2:遍历inDegree数组,将所有入度为0的节点入nodes队列; step3:依次将节点node出队; 根据visited判断当前node是否已经被访问,是,返回step3,否,进行下一步; 将当前节点的邻接节点入度-1,判断邻接节点入度是否为0,为0直接放入nodes队列,不为0返回step3;
/**
* @param graph 有向无环图
* @return 拓扑排序结果
*/
public List<Character> toPoLogicalSort(Graph graph) {
//用一个数组标志所有节点入度
int[] inDegree = new int[graph.nodeSize];
for (LinkedList list : graph.adj) {
for (Object index : list) {
++ inDegree[(int)index];
}
}
//用一个数组标志所有节点是否已经被访问
boolean[] visited = new boolean[graph.nodeSize];
//开始进行遍历
Deque<Integer> nodes = new LinkedList<>();
//将入度为0节点入队
for (int i = 0 ; i < graph.nodeSize; i++) {
if (inDegree[i] == 0) {
nodes.offer(i);
}
}
List<Character> result = new ArrayList<>();
//将入度为0节点一次出队处理
while (!nodes.isEmpty()) {
int node = nodes.poll();
if (visited[node]) {
continue;
}
visited[node] = true;
result.add(graph.node[node]);
//将当前node的邻接节点入度-1;
for (Object list : graph.adj[node]) {
-- inDegree[(int)list];
if (inDegree[(int)list] == 0) {
//前驱节点全部访问完毕,入度为0
nodes.offer((int) list);
}
}
}
return result;
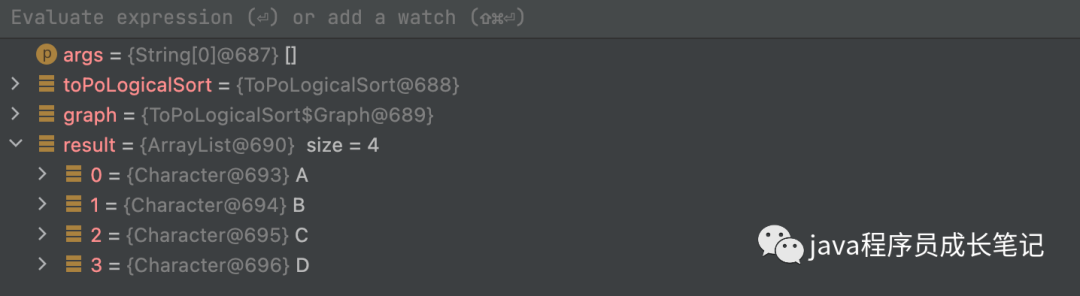
}测试样例1
public static void main(String[] args) {
ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
//初始化一个图
Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D'});
graph.addEdge(0, 1);
graph.addEdge(0,2);
graph.addEdge(1,3);
graph.addEdge(2,3);
List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
}执行结果
测试样例2
public static void main(String[] args) {
ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
//初始化一个图
Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D','E','F','G','H'});
graph.addEdge(0, 1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(2,4);
graph.addEdge(3,4);
graph.addEdge(4,7);
graph.addEdge(4,6);
graph.addEdge(7,5);
graph.addEdge(6,7);
List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
}执行结果

总结
我在上面有说到,拓扑排序可以用来判断图是否存在环,其实判断方式很简单,实现步骤与上面一致,只是我们最后判断一下出队的元素个数是否等于图的节点个数,如果等于,证明图无环,如果不等于则证明存在环。
到此这篇关于Java实现拓扑排序的示例代码的文章就介绍到这了,更多相关Java拓扑排序内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
相关文章

深入理解Java8新特性之Stream API的终止操作步骤
Stream是Java8的一大亮点,是对容器对象功能的增强,它专注于对容器对象进行各种非常便利、高效的 聚合操作(aggregate operation)或者大批量数据操作。Stream API借助于同样新出现的Lambda表达式,极大的提高编程效率和程序可读性,感兴趣的朋友快来看看吧2021-11-11












最新评论