Python实现曲线的肘部点检测详解
更新时间：2023年02月28日 09:48:20 作者：mantoureganmian
肘部法则是经常使用的法则。很多时候，可以凭人工经验去找最优拐点，但有时需要自动寻找拐点。本文为大家介绍了Python实现曲线的肘部点检测的方法，希望对大家有所帮助
肘部法则是经常使用的法则。很多时候，可以凭人工经验去找最优拐点，但有时需要自动寻找拐点。最近解决了一下这个问题，希望对各位有用。
一. 术语解释
**肘形曲线(elbow curve)**类似人胳膊状的曲线，拐点在肘部。**膝形曲线（knee curve）人腿形的曲线，拐点在膝盖。这类曲线和二八原则（即帕托累法则）**不谋而合，做决策时，自然选择肘点或膝点做参考。按照拐点在左还是右侧来分，细分为：左膝点曲线，右膝点曲线，左肘点曲线，右肘点曲线。
曲线示意图如下：
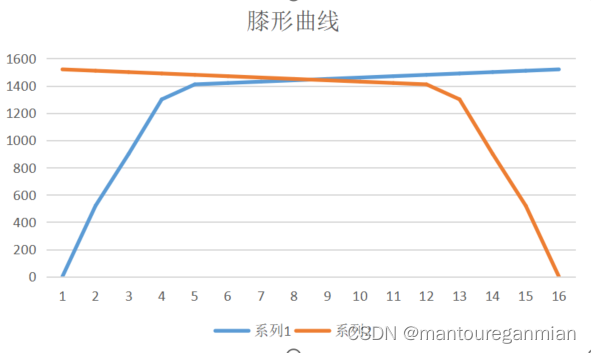
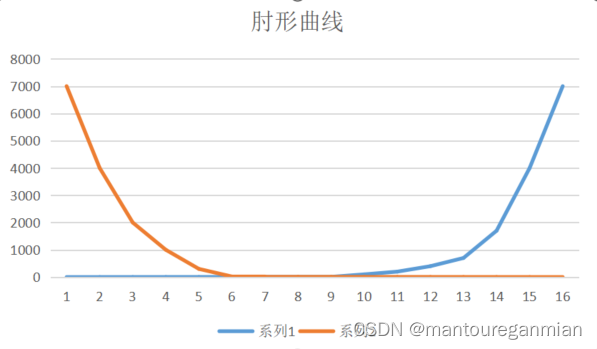
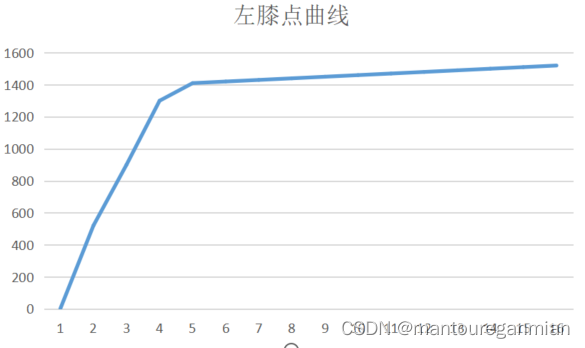
左膝点曲线膝点在左边的曲线（术语是我自己起的，明白意思就好，膝点在左边）如下：
从形状上，四种曲线没有大的区别，可以相互转化：
肘曲线与膝曲线相互转化，用曲线最大值减去曲线各点值即可。同类型曲线，左右拐点转化，就是切换升序降序排序即可。
它们都可以计算拐点，其中以左膝点曲线(见下图)计算拐点最简单，所以以其为标准曲线。
二. 拐点检测
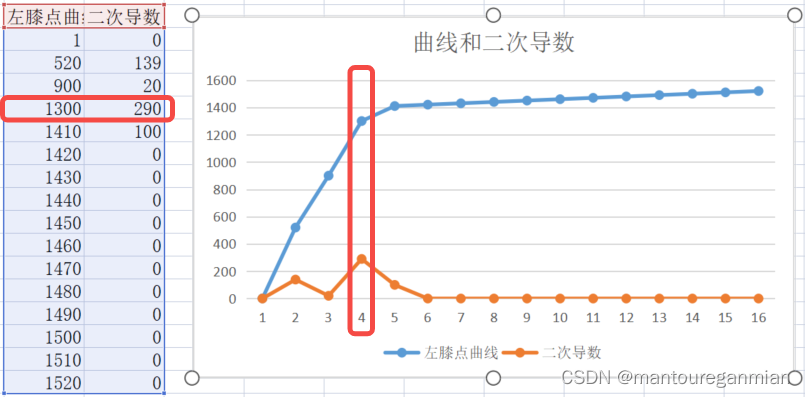
左膝点曲线，原理是其二次曲线导数最大点，如下：
对于离散序列来说，当x轴差为1时，二次曲线计算公式为：
f′′(xi)=f(xi−1)+f(xi+1)−2*f(xi)
推荐一个简单的包：kneed Github地址
支持:Python 3.7, 3.8, 3.9, and 3.10. 安装如下：
$ conda install -c conda-forge kneed # 或者 $ pip install kneed # To install only knee-detection algorithm $ pip install kneed[plot] # To also install plotting functions for quick
使用如下：
from kneed import DataGenerator, KneeLocator x, y = DataGenerator.figure2() print([round(i, 3) for i in x]) print([round(i, 3) for i in y]) # out: [0.0, 0.111, 0.222, 0.333, 0.444, 0.556, 0.667, 0.778, 0.889, 1.0] # out: [-5.0, 0.263, 1.897, 2.692, 3.163, 3.475, 3.696, 3.861, 3.989, 4.091] kneedle = KneeLocator(x, y, S=1.0, curve="concave", direction="increasing") print(round(kneedle.knee, 3)) # out: 0.222 print(round(kneedle.elbow, 3)) # out: 0.222
到此这篇关于Python实现曲线的肘部点检测详解的文章就介绍到这了,更多相关Python曲线肘部点检测内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！
相关文章
python视频高速传输程序,大家参考使用吧2013-12-12
使用 Python 的 pprint库格式化和输出列表和字典的方法
pprint是"pretty-print"的缩写，使用 Python 的标准库 pprint 模块，以干净的格式输出和显示列表和字典等对象，这篇文章主要介绍了如何使用 Python 的 pprint库格式化和输出列表和字典,需要的朋友可以参考下2023-05-05
这篇文章主要介绍了Python3 实现建造者模式的示例代码，文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值，需要的朋友们下面随着小编来一起学习学习吧2020-06-06
这篇文章主要介绍了提升Python效率之使用循环机制代替递归函数的相关知识，本文给大家介绍的非常详细，具有一定的参考借鉴价值,需要的朋友可以参考下2019-07-07
在Python中获取IP地址的方法有很多种,这篇文章主要给大家介绍了关于Python获取ip地址的3种方法,文中通过代码介绍的非常详细,需要的朋友可以参考下2023-10-10
在本篇内容里小编给大家整理了关于django教程学习流程，想自学的朋友们可以阅读下。2020-07-07
这篇文章主要给大家介绍了关于Python面经之16个高频面试问题的相关资料,帮助大家回顾基础知识,了解面试套路,对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下2022-03-03
这篇文章主要介绍了python创建线程示例,需要的朋友可以参考下2014-05-05
命令行参数是通过sys.argv[]来获取的，sys.argv[0]是代码文件本身的路径，因此参数是从1开始的。比如设置参数为： spe2008-09-09
这篇文章主要介绍了python实现下载指定网址所有图片的方法,涉及Python针对页面的读取、遍历及文件操作的相关技巧,具有一定参考借鉴价值,需要的朋友可以参考下2015-08-08
最新评论