十进制负数转换为二进制、八进制、十六进制的知识分享

程序猿们或许对二进制都不陌生，二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。但是很多人都会将二进制转换成整数，但是如何用二进制表示负数呢？有的人会说，在二进制前面加个负数符合。而计算机只能认识0 和 1，又怎么去加个额外的负数符号呢？于是我们就需要用0和1来表示负数。如果想要弄懂这个，我们需要先了解什么是二进制原码。

原码(true form)是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位（即最高位为符号位）：正数该位为0，负数该位为1（0有两种表示：+0和-0），其余位表示数值的大小。

简单直观；例如，我们用8位二进制表示一个数，+11的原码为00001011，-11的原码就是10001011

原码不能直接参加运算，可能会出错。例如数学上，1+(-1)=0，而在二进制中00000001 + 10000001 = 10000010，换算成十进制为-2。显然出错了。

二进制原码、补码和反码

我们如何把十进制的-3，转换成二进制表示呢？首先我们将 -3 的绝对值 +3 转换成二进制，假设是为int类型(32位)的，那么二进制表示为：

0000 0000 0000 0000 0000 0000 0000 0011

负数转换成二进制分为3步：

1、 首先将负数转换为对应的原码

-3 的原码为(也就是+3转换成二进制后的字符串)：

0000 0000 0000 0000 0000 0000 0000 0011

2、 再将原码的每一位做取反操作得到反码。

取反操作：0变为1 、 1变为0；取反后的结果即为：

1111 1111 1111 1111 1111 1111 1111 1100

3、 将反码+1得到补码

1111 1111 1111 1111 1111 1111 1111 1101

现在用Windows自带的计算器来验证一下，Win+R 输入calc，将计算器改为程序员，选择双字(4字节,32位)

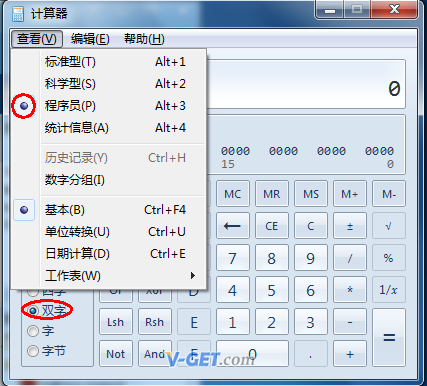
打开Windows自带的计算器科学计算功能

在计算器中选择十进制，之后输入 -3 ：

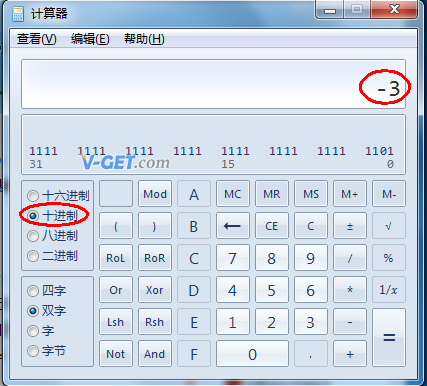
Windows自带的计算器科学计算十进制下输入-3

再点击二进制转换，将十进制下的-3转换成二进制：

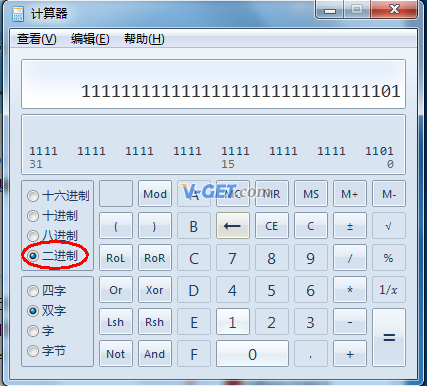
转换十进制-3为二进制

正常情况下，转换二进制到十进制都是没有任何问题的。而在类似 Javascript / PHP 等整数类型中，一般 int /integer 都有位数限制，一般都是32位长度。也就预示着，这些语言中，整数是有最大值的，而32位最大整数极限为：2147483647，也就是二进制：

01111111111111111111111111111111

那么就很容易理解，32位二进制，第一位数为0的时候，就表示这个是一个正数，而如果是1，那么就表示这个是负数。

32位二进制 11111111111111111111111111111001 十进制值是什么？

11111111111111111111111111111001

如上，二进制长度为32位，也就是这个整数是一个负数，先取反，得到反码：

00000000000000000000000000000110

反码+1，得到：

00000000000000000000000000000111

转换成十进制：7

由于是负数，所以加个负号，转换成 -7

趣味：32位二进制 1111111111111111111111111111001 十进制值是什么？

这个是个比较有趣的，千万不要误导为上面这是一个负数，其实这个是个整数，因为这里只有31位，需要在前面加0，补足32位，变成：

01111111111111111111111111111001

负数转换成八进制、十六进制，只需在补码(二进制)的基础上，3位合成一位计算，或者4位合成一位计算

-3的转换成二进制为：

1111 1111 1111 1111 1111 1111 1111 1101

八进制则将-3的二进制从右至左每3位为一个单元，不够三位用0补 即：

011 111 111 111 111 111 111 111 111 111 101

计算每一个单元，结果为：37777777775

十六进制则将-3的二进制从右至左每4位合并为一个单元，即：

1111 1111 1111 1111 1111 1111 1111 1101

计算后为： FFFFFFFD

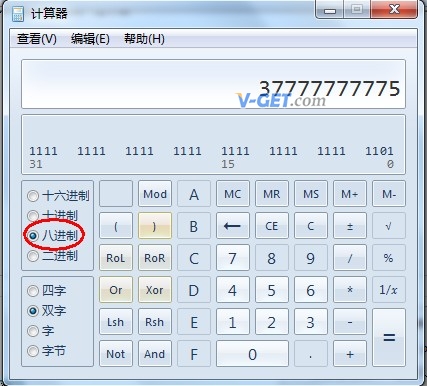
转换十进制-3为八进制和十六进制

最新评论