C语言实现二叉树的示例详解
二叉树的遍历算法
先序遍历算法
先序遍历的实现方式在前面已经说过了,比如下面的一棵二叉树:
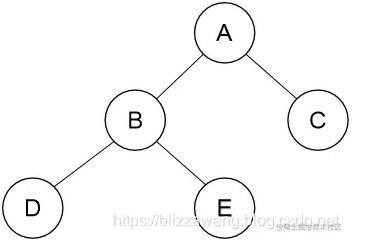
我们需要先访问根结点A,然后以先序遍历的方式遍历左子树,左子树同样是一棵二叉树,以同样的方式访问根结点B,然后先序遍历B的左子树,会发现,这是一个递归的过程,所以我们可以通过递归实现。 先序遍历算法实现如下:
void PreOrderTraverse(BiTree t){
//判断当前结点是否为空
if(t == NULL){
return;
}
//输出根结点
printf("%c\t",t->data);
//先序遍历左子树
PreOrderTraverse(t->lchild);
//先序遍历右子树
PreOrderTraverse(t->rchild);
}代码实现非常简单,但是需要一定的时间理解: 我们首先传入二叉树的根结点,根结点不为空,所以输出A,此时调用自身,将左孩子传入,此时将先序遍历左子树。 传入结点B依然不为空,此时输出B,然后又调用自身,将结点B的左孩子传入,此时将先序遍历结点B的左子树。 传入结点D依然不为空,此时输出D,然后又调用自身,将结点D的左孩子传入,此时左孩子为空,所以函数返回,返回后就执行先序遍历右子树,传入的右孩子仍然为空,此时继续返回,先序遍历结点B的右孩子。 以此类推,注意理解。
我们来测试一下,因为刚刚接触遍历算法,所以这里,我们通过一个比较笨的方式实现二叉树,然后调用先序遍历函数:
int main(){
//创建根结点
BiTree root = (BiTree) malloc(sizeof(BiNode));
root->data = 'A';
//创建根结点的左孩子
root->lchild = (BiTree) malloc(sizeof(BiNode));
root->lchild->data = 'B';
//创建根结点的右孩子
root->rchild = (BiTree) malloc(sizeof(BiNode));
root->rchild->data = 'C';
//创建根结点的左孩子的左孩子
root->lchild->lchild = (BiTree) malloc(sizeof(BiNode));
root->lchild->lchild->data = 'D';
//创建根结点的左孩子的右孩子
root->lchild->rchild = (BiTree) malloc(sizeof(BiNode));
root->lchild->rchild->data = 'E';
//根结点的右孩子无左右孩子
root->rchild->lchild = NULL;
root->rchild->rchild = NULL;
//根结点的左孩子的左孩子无左右孩子
root->lchild->lchild->lchild = NULL;
root->lchild->lchild->rchild = NULL;
//根结点的左孩子右孩子无左右孩子
root->lchild->rchild->lchild = NULL;
root->lchild->rchild->rchild = NULL;
//先序遍历
PreOrderTraverse(root);
return 0;
}运行结果:
A B D E C
中序遍历算法
中序遍历和后序遍历的算法就不用分析了,过程是一样的,只不过是操作根结点的顺序变了。 中序遍历算法实现如下:
void InOrderTraverse(BiTree t){
//判断当前结点是否为空
if(t == NULL){
return;
}
//先序遍历左子树
InOrderTraverse(t->lchild);
//输出根结点
printf("%c\t",t->data);
//先序遍历右子树
InOrderTraverse(t->rchild);
}后序遍历算法
后序遍历算法实现如下:
void PostOrderTraverse(BiTree t){
//判断当前结点是否为空
if(t == NULL){
return;
}
//先序遍历左子树
PostOrderTraverse(t->lchild);
//先序遍历右子树
PostOrderTraverse(t->rchild);
//输出根结点
printf("%c\t",t->data);
}非递归遍历算法
遍历思想
前面介绍了三种遍历算法,都是通过递归实现的,虽然递归实现的代码量非常少,但是递归较难理解,而且空间消耗大,所以这里我也介绍一下遍历算法的非递归实现,具体想用哪种办法就看自己了。
这里以中序遍历算法的非递归实现作为例子重点讲述。 当然思想还是一样的,我们需要优先遍历左子树,然后访问根结点,最后访问右子树,既然是这样,根结点我们就需要先保存下来,这里可以用栈实现。 比如下面的这棵二叉树:
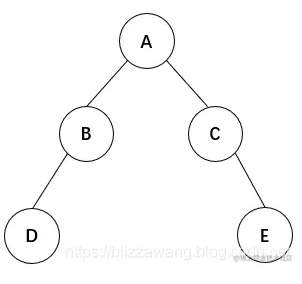
如何实现非递归的中序遍历呢?
中序遍历算法是先遍历左子树,然后访问根结点的,所以一开始传入根结点A,我们不能访问,此时将根结点A入栈,然后遍历根结点A的左子树。

此时以同样的方式遍历左子树,遇到左子树的根结点B,同样不能访问,将根结点B入栈,然后遍历根结点B的左子树。
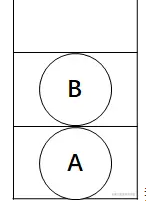
我们接着遍历结点B的左子树,同样将根结点D入栈。
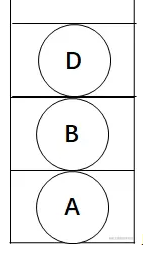
此时结点D无左孩子,这样就可以访问根结点了,对栈进行出栈操作,因为栈的特性,此时出栈结点为D。
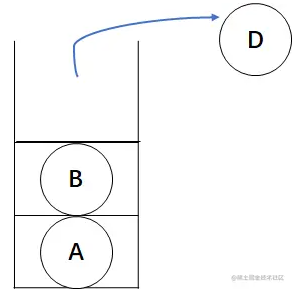
然后遍历根结点D的右子树,因为结点D无右孩子,此时需要退回到结点B,这时候结点B的左子树已经遍历完了,可以访问根结点了,对栈进行出栈操作,出栈结点为B。
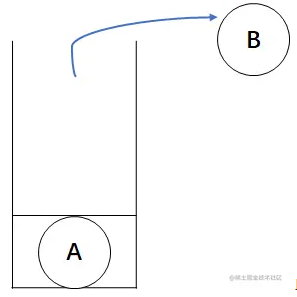
此时根结点A的左子树也遍历完了,又进行出栈操作,出栈结点为A。

以同样的方式遍历右子树,遇到结点C,先入栈,然后访问其左子树,结点C无左孩子,所以结点C出栈,接着遍历右子树,以此类推。
遍历结果为:D B A C E
算法实现
实现思想讲解清楚了,接下来是算法实现,在实现这个算法之前我们还需要实现一个栈结构,这里采用顺序栈。
#define TElemType char
int top=-1;//top变量时刻表示栈顶元素所在位置
//构造结点的结构体
typedef struct BiTNode{
TElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
//前序和中序遍历使用的进栈函数
void push(BiTNode** a,BiTNode* elem){
a[++top]=elem;
}
//弹栈函数
void pop( ){
if (top==-1) {
return ;
}
top--;
}
//模拟操作结点元素的函数,输出结点本身的数值
void displayElem(BiTNode* elem){
printf("%c ",elem->data);
}
//拿到栈顶元素
BiTNode* getTop(BiTNode**a){
return a[top];
}
//中序遍历非递归实现
void InOrderTraverse(BiTree Tree){
BiTNode* a[20];//定义一个顺序栈
BiTNode * p;//临时指针
p=Tree;
//当p为NULL并且栈为空时,表明树遍历完成
while (p != NULL || top!=-1) {
//如果p不为NULL,将其压栈并遍历其左子树
if (p != NULL) {
push(a, p);
p=p->lchild;
}
//如果p==NULL,表明左子树遍历完成,需要遍历上一层结点的右子树
else{
p=getTop(a);
pop();
displayElem(p);
p=p->rchild;
}
}
}层次遍历算法
层次遍历算法是通过二叉树的层次决定的,如下面的一棵二叉树:
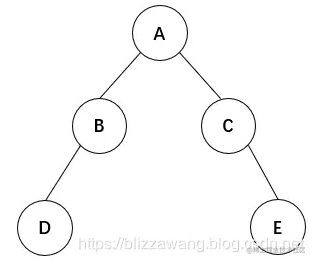
它的层次遍历结果为:A B C D E,即从上到下,从左到右进行遍历。 对于层次遍历,我们可以使用队列实现。 首先传入根结点A,此时将根结点A入队,然后就可以执行出队操作,出队结点为A;

出队之后判断根结点A是否有左右孩子,如果有,则将结点B、C分别入队,然后执行出队操作,由于队列的特性,出队结点为B;

结点B出队之后判断结点B是否有左右孩子,有左孩子,则入队,然后执行出队操作,出队结点为C;

继续判断结点C是否有左右孩子,结点C有右孩子E,将结点E入队,然后执行出队操作,出队结点为D;

判断结点D是否有左右孩子,结点D无左右孩子,直接执行出队操作,出队结点为E; 结点E也无左右孩子,而队列也已经空了,此时遍历完成。
该算法和刚才介绍的非递归遍历算法有异曲同工之妙,这里就不具体写出该算法了,大家可以尝试着自己实现一下。
先序遍历建立二叉树算法
在学习遍历算法的时候,还记得我们是如何建立二叉树的吗?
int main(){
//创建根结点
BiTree root = (BiTree) malloc(sizeof(BiNode));
root->data = 'A';
//创建根结点的左孩子
root->lchild = (BiTree) malloc(sizeof(BiNode));
root->lchild->data = 'B';
//创建根结点的右孩子
root->rchild = (BiTree) malloc(sizeof(BiNode));
root->rchild->data = 'C';
//创建根结点的左孩子的左孩子
root->lchild->lchild = (BiTree) malloc(sizeof(BiNode));
root->lchild->lchild->data = 'D';
//创建根结点的左孩子的右孩子
root->lchild->rchild = (BiTree) malloc(sizeof(BiNode));
root->lchild->rchild->data = 'E';
//根结点的右孩子无左右孩子
root->rchild->lchild = NULL;
root->rchild->rchild = NULL;
//根结点的左孩子的左孩子无左右孩子
root->lchild->lchild->lchild = NULL;
root->lchild->lchild->rchild = NULL;
//根结点的左孩子右孩子无左右孩子
root->lchild->rchild->lchild = NULL;
root->lchild->rchild->rchild = NULL;
return 0;
}可以看到,这个方法非常麻烦,但是建立算法又建立在遍历算法之上,所以我们应该先掌握遍历算法,再来学习建立算法。
先序遍历建立算法即通过一个先序的遍历序列建立出一棵二叉树,比如下面的一个先序序列: A B C D E G F 需要注意的是,单凭这个先序序列并不能唯一确定一棵二叉树。

比如这两棵二叉树的先序遍历结果均为:A B C D E G F。 所以我们需要对这棵二叉树进行补充,补充一些空结点,然后按照顺序进行建立:
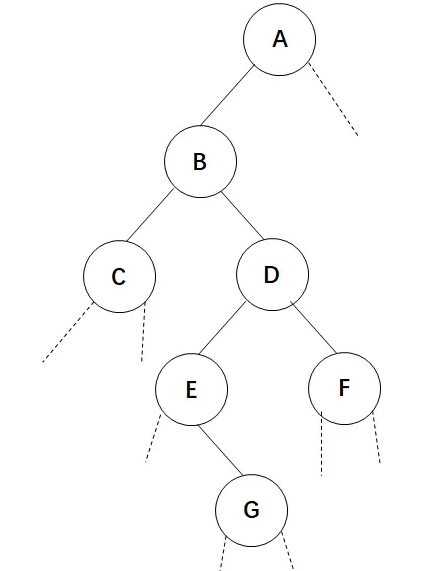
先序遍历建立二叉树算法实现如下:
BiTree CreateBiTreePre(){
BiTree root;
char ch;
printf("请输入结点数据:\n");
scanf("%c",&ch);
getchar(); //接收一个回车
if(ch == '#'){
root = NULL;
}else{
//创建结点
root = (BiTree) malloc(sizeof(BiNode));
root->data = ch;
//递归建立左子树
root->lchild = CreateBiTreePre();
//递归建立右子树
root->rchild = CreateBiTreePre();
}
return root;
}测试一下:
int main(){
BiTree root;
//先序建立二叉树
root = CreateBiTreePre();
printf("先序遍历:");
PreOrderTraverse(root);
printf("\n");
printf("中序遍历:");
InOrderTraverse(root);
printf("\n");
printf("后序遍历:");
PostOrderTraverse(root);
return 0;
}运行程序,输入:A B C # # D E # G # # F # # # 运行结果:
先序遍历:A B C D E G F
中序遍历:C B E G D F A
后序遍历:C G E F D B A
遍历二叉树算法的应用
下面介绍一下遍历二叉树算法的应用。
复制二叉树
通过遍历一棵二叉树,我们能够将一棵二叉树复制到另一棵二叉树上。
BiTree CopyTree(BiTree t){
BiTree newT;
if(t == NULL){
return NULL;
}else{
//创建新结点
newT = (BiTree) malloc(sizeof(BiNode));
if(newT == NULL){
exit(-1);
}
//复制结点的数据域
newT->data = t->data;
//递归复制左子树
newT->lchild=CopyTree(t->lchild);
//递归复制右子树
newT->rchild=CopyTree(t->rchild);
return newT;
}
}中序和后序复制二叉树的实现与其类似,不重复讨论。
计算二叉树的深度
遍历二叉树算法还可以用于计算二叉树的深度,算法如下:
int Depth(BiTree t){
int m,n;
//判断二叉树是否为空
if(t == NULL){
return 0; //深度为0
}
//计算左子树深度
m = Depth(t->lchild);
//计算右子树深度
n = Depth(t->rchild);
//判断左右子树哪棵树深度最大,最后记得加1(加的是根结点)
if(m > n){
return m + 1;
}else{
return n + 1;
}
}这些算法都比较简单,就不一一分析了,看代码注释应该就能够理解了。
计算二叉树的结点总数
遍历算法因为要访问二叉树中的每个结点,所以它还能够用于计算结点总数,算法实现如下:
int GetNodeCount(BiTree t){
if(t == NULL){ //若当前结点为NULL,返回0
return 0;
}
//返回左子树结点数 + 右子树结点数 + 根结点
return GetNodeCount(t->lchild) + GetNodeCount(t->rchild) + 1;
}计算二叉树的叶子结点数
计算叶子结点数的方式和刚才的算法类似,下面是代码实现:
int GetLeafCount(BiTree t){
if(t == NULL){ //若当前结点为NULL,返回0
return 0;
}
if(t->lchild == NULL && t->rchild == NULL){
//若当前结点无左右孩子,则表明是叶子结点
return 1;
}
//返回左子树叶子结点数 + 右子树叶子结点数
return GetLeafCount(t->lchild) + GetLeafCount(t->rchild);
}线索二叉树的由来
先来看下面这棵二叉树:
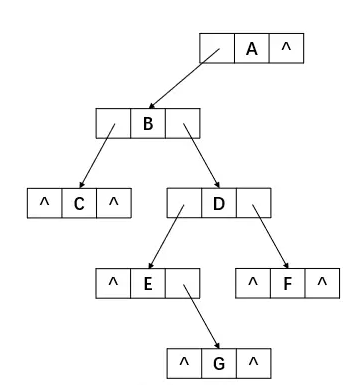
这是二叉树存储结构中的二叉链表,其优点是能够很方便地找到任意结点的左右孩子,然而,它也有缺点:一般情况下,无法直接找到某个结点在某种遍历序列下的前驱结点和后继结点。
为了能够方便地找到任意结点的前驱和后继结点,我们可以在结点中保存其前驱和后继的结点地址,但如果为其增设两个指针域显然会牺牲很多空间,为此,我们可以利用二叉链表中的空指针域。
假设一棵具有n个结点的二叉树,其一共有2n个指针域,而n个结点的二叉树有n - 1个孩子结点,也就是说,该二叉树一共使用了n - 1个指针域用来指向左右孩子,这样就有n + 1个指针域是空着的,我们刚好可以利用这些指针域,用它们指向结点的前驱或者后继结点。
如何利用二叉链表中的空指针域
对于一棵二叉树的二叉链表结构,若某个结点的左孩子为空,则将空的左孩子指针域指向其前驱结点;同理,若某个结点的右孩子为空,则将空的友好孩子指针域指向其后继结点。我们将这种改变指向的指针称为"线索",加上了线索的二叉树称为线索二叉树。
看这样的一个例子,比如下面的一棵二叉树:

我们说二叉树的线索化是相对于某个遍历序列而言的,上面这棵二叉树的中序遍历结果为:C B E G D F A 则对于中序遍历序列来说,该如何实现线索化呢?
先看结点A,其右孩子指针域为空,此时我们应该利用起来这个空指针域,让其指向它的后继结点,而从中序遍历结果得知,结点A无后继结点,所以我们最后还是让结点A的右孩子指针域为空,不作处理。
再看结点C,其左右孩子指针域均为空,此时我们先处理左孩子指针域。从中序遍历结果得知,结点C无前驱结点,但其后继结点为B,所以我们不对左孩子指针域作处理,而让右孩子指针域指向结点B。

继续看结点E,其左孩子指针域为空,而其前驱结点为B,所以让其左孩子指针域指向结点B。
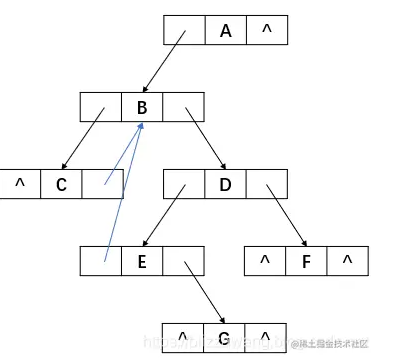
处理结点F和结点G的方式也是一样的,最后线索化完成的结果应为:

看到线索化后的二叉树,很多同学可能懵了,这么多的指针指向,到底哪些是指向前驱和后继结点的,哪些是指向孩子结点的呢?
为了区分,我们可以对二叉链表的结点结构增设两个标志域ltag和rtag,并作出如下约定:
- ltag = 0,lchild指向该结点的左孩子
- ltag = 1,lchild指向该结点的前驱
- rtag = 0,rchild指向该结点的右孩子
- rtag = 1,rchild指向该结点的后继
所以其结点结构应为:
typedef struct BiThrNode{
char data;
struct BiThrNode *lchild,*rchild;
int ltag,rtag; //标志域
}BiThrNode,*BiThrTree;看下面的一棵二叉树:

对其进行先序线索化,先得出先序遍历结果:A B C D E,其线索化结果为:

其中序线索化结果为(中序遍历结果:B C A E D):
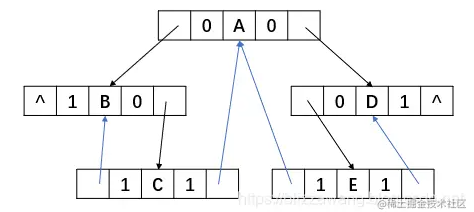
后序线索化就留给大家自己画一画了。
到此这篇关于C语言实现二叉树的示例详解的文章就介绍到这了,更多相关C语言二叉树内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
相关文章

使用VS2022开发在线远程编译部署的C++程序(图文详解)
这篇文章主要介绍了使用VS2022开发可以在线远程编译部署的C++程序,本文分步骤通过图文并茂的形式给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要的朋友可以参考下2021-12-12












最新评论