一文带你搞懂C++中的流量控制
流量控制
一般并发系统有对应处理请求的最大能力，这里称最大qps，也需要有阈值设置，如果超过最大qps，则可能导致系统不稳定，产生雪崩效应，甚至连锁反应。
限流可以认为服务降级的一种，限流就是限制系统的输入和输出流量已达到保护系统的目的。一般来说系统的吞吐量是可以被测算的，为了保证系统的稳定运行，一旦达到的需要限制的阈值，就需要限制流量并采取一些措施以完成限制流量的目的。比如：部分拒绝处理。
这也是最常见的场景，流控是为了保护下游有限的资源不被流量冲垮，保证服务的可用性，一般允许流控的阈值有一定的弹性，偶尔的超量访问是可以接受的。
有的场景下，流控服务于收费模式，比如某些云厂商会对调用 API 的频次进行计费。既然涉及到钱，一般不允许有超出阈值的调用量。
1 固定窗口
流控是为了限制指定时间间隔内能够允许的访问量，因此，最直观的思路就是基于一个给定的时间窗口，维护一个计数器用于统计访问次数，然后实现以下规则：
- 如果访问次数小于阈值，则代表允许访问，访问次数 +1。
- 如果访问次数超出阈值，则限制访问，访问次数不增。
- 如果超过了时间窗口，计数器清零，并重置清零后的首次成功访问时间为当前时间。这样就确保计数器统计的是最近一个窗口的访问量。
代码实现
#include <chrono>
#include <cstdint>
#include <cstdio>
#include <ctime>
#include <thread>
const int NS_PER_SECOND = 1e9;
// 获取当前时间戳, 单位纳秒
int64_t Now() {
struct timespec ts;
clock_gettime(CLOCK_MONOTONIC, &ts);
return ts.tv_sec * NS_PER_SECOND + ts.tv_nsec;
}
class RateLimiter {
// 时间窗口, 单位秒
int64_t window_;
// 时间窗口内最大允许的阈值
int64_t threshold_;
// 当前时间窗口的起始时间
int64_t start_time_ = Now();
// 计数器
int64_t counter_;
public:
RateLimiter(int64_t window, int64_t threshold)
: window_(window), threshold_(threshold) {}
/**
* @param permits 配额数量
* @return 申请成功则返回true，否则返回false
*/
bool tryAcquire(int permits) {
long now = Now();
if (now - start_time_ > window_ * NS_PER_SECOND) {
counter_ = 0;
start_time_ = now;
}
if (counter_ + permits <= threshold_) {
counter_ += permits;
return true;
} else {
return false;
}
}
};
int main() {
// 限流300MB/s
RateLimiter limiter(1, 300 * 1024 * 1024);
// 每次请求256KB
int64_t request_size = 256 * 1024;
// 每隔约1ms发起2次请求
// 每隔1s打印一次请求数据量
int64_t start_time = Now();
int64_t last_time = start_time;
int64_t last_size = 0;
while (true) {
int64_t now = Now();
if (now - last_time >= NS_PER_SECOND) {
printf("time: %lf s, request size: %lf MB\n", (now - last_time) / 1e9,
(last_size / 1024.0 / 1024.0));
last_time = now;
last_size = 0;
}
for (int i = 0; i < 2; ++i) {
if (limiter.tryAcquire(request_size)) {
last_size += request_size;
}
}
std::this_thread::sleep_for(std::chrono::milliseconds(1));
}
return 0;
}
注意: 示例为单线程，多线程需要考虑线程安全问题。
临界突变问题
固定窗口的流控实现非常简单，以 1 分钟允许 100 次访问为例，如果流量均匀保持 200 次/分钟的访问速率，系统的访问量曲线大概是这样的（按分钟清零）：
但如果流量并不均匀，假设在时间窗口开始时刻 0:00 有几次零星的访问，一直到 0:50 时刻，开始以 10 次/秒的速度请求，就会出现这样的访问量图线：
在临界的 20 秒内（0:50~1:10）系统承受的实际访问量是 200 次，换句话说，最坏的情况下，在窗口临界点附近系统会承受 2 倍的流量冲击，这就是固定窗口不能解决的临界突变问题。
2 滑动窗口
如何解决固定窗口算法的临界突变问题？既然一个窗口统计的精度低，那么可以把整个大的时间窗口切分成更细粒度的子窗口，每个子窗口独立统计。同时，每过一个子窗口大小的时间，就向右滑动一个子窗口。这就是滑动窗口算法的思路。
如上图所示，将一分钟的时间窗口切分成 6 个子窗口，每个子窗口维护一个独立的计数器用于统计 10 秒内的访问量，每经过 10s，时间窗口向右滑动一格。
回到固定窗口出现临界跳变的例子，结合上面的图再看滑动窗口如何消除临界突变。如果 0:50 到 1:00 时刻（对应灰色的格子）进来了 100 次请求，接下来 1:00~1:10 的 100 次请求会落到黄色的格子中，由于算法统计的是 6 个子窗口的访问量总和，这时候总和超过设定的阈值 100，就会拒绝后面的这 100 次请求。
(代码实现请参考 Sentinel)
精度问题
现在思考这么一个问题：滑动窗口算法能否精准地控制任意给定时间窗口 T 内的访问量不大于 N？
答案是否定的，还是将 1 分钟分成 6 个 10 秒大小的子窗口的例子，假设请求的速率现在是 20 次/秒，从 0:05 时刻开始进入，那么在 0:050:10 时间段内会放进 100 个请求，同时接下来的请求都会被限流，直到 1:00 时刻窗口滑动，在 1:001:05 时刻继续放进 100 个请求。如果把 0:05~1:05 看作是 1 分钟的时间窗口，那么这个窗口内实际的请求量是 200，超出了给定的阈值 100。
如果要追求更高的精度，理论上只需要把滑动窗口切分得更细。像 Sentinel 中就可以通过修改单位时间内的采样数量 sampleCount 值来设置精度，这个值一般根据业务的需求来定，以达到在精度和内存消耗之间的平衡。
平滑度问题
使用滑动窗口算法限制流量时，我们经常会看到像下面一样的流量曲线。
突发的大流量在窗口开始不久就直接把限流的阈值打满，导致剩余的窗口内所有请求都无法通过。在时间窗口的单位比较大时（例如以分为单位进行流控），这种问题的影响就比较大了。在实际应用中我们要的限流效果往往不是把流量一下子掐断，而是让流量平滑地进入系统当中。
3 漏桶
滑动窗口无法很好地解决平滑度问题，再回过头看我们对于平滑度的诉求，当流量超过一定范围后，我们想要的效果不是一下子切断流量，而是将流量控制在系统能承受的一定的速度内。假设平均访问速率为 v, 那我们要做的流控其实是流速控制，即控制平均访问速率 v ≤ N / T。
在网络通信中常常用到漏桶算法来实现流量整形。漏桶算法的思路就是基于流速来做控制。想象一下上学时经常做的水池一边抽水一边注水的应用题，把水池换成水桶（还是底下有洞一注水就开始漏的那种），把请求看作是往桶里注水，桶底漏出的水代表离开缓冲区被服务器处理的请求，桶口溢出的水代表被丢弃的请求。在概念上类比：
- 最大允许请求数 N ：桶的大小
- 时间窗口大小 T ：一整桶水漏完的时间
- 最大访问速率 V ：一整桶水漏完的速度，即 N/T
- 请求被限流 ：桶注水的速度比漏水的速度快，最终桶满了, 装不了水
假设起始时刻桶是空的，每次访问都会往桶里注入一单位体积的水量，那么当我们以小于等于 N/T 的速度往桶里注水时，桶内的水就永远不会溢出。反之，一旦实际注水速度超过漏水速度，桶里就会积累越来越多的水，直到桶满。同时漏水的速度永远被控制在 N/T 以内，这就实现了平滑流量的目的。
漏桶算法的访问速率曲线如下：
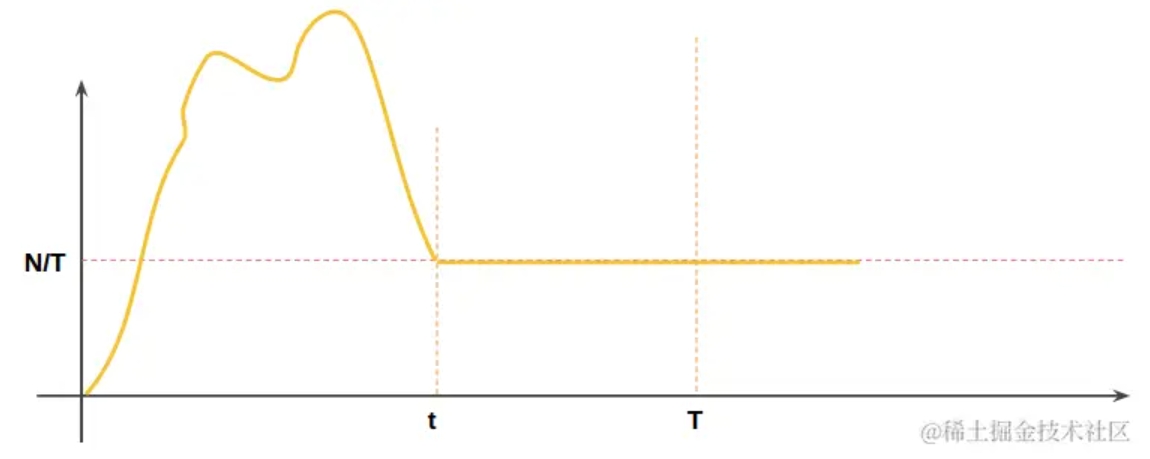
附上一张网上常见的漏桶算法原题图：
代码实现 LeakyBucket
class LeakyBucket {
int64_t last_time_ = Now();
int64_t rate_;
int64_t debt_;
// 精度
int64_t precision_;
int64_t quota_;
public:
LeakyBucket(int64_t rate, double precision = 1000)
: rate_(rate), precision_(precision) {
quota_ = rate_ / precision_;
}
bool tryAcquire(int permits) {
int64_t now = Now();
int64_t pay_off = (now - last_time_) * rate_ / NS_PER_SECOND;
int64_t left_debt = std::max(0LL, debt_ - pay_off);
if (left_debt > quota_) {
return false;
}
debt_ = left_debt + permits;
last_time_ = now;
return true;
}
};
class LeakyBucket {
int64_t last_time_ = Now();
int64_t rate_;
int64_t debt_;
// 精度
int64_t precision_;
int64_t quota_;
public:
LeakyBucket(int64_t rate, double precision = 1000)
: rate_(rate), precision_(precision) {
quota_ = rate_ / precision_;
}
bool tryAcquire(int permits) {
int64_t now = Now();
int count = (now - last_time_) / (NS_PER_SECOND / precision_);
int64_t pay_off = count * quota_;
int64_t left_debt = std::max(0LL, debt_ - pay_off);
if (left_debt > quota_) {
return false;
}
debt_ = left_debt + permits;
last_time_ += count * (NS_PER_SECOND / precision_);
return true;
}
};
漏桶的问题
漏桶的优势在于能够平滑流量，如果流量不是均匀的，那么漏桶算法与滑动窗口算法一样无法做到真正的精确控制。
虽然可以通过限制桶大小的方式使得访问量控制在 N 以内，但这样做的副作用是流量在还未达到限制条件就被禁止。
还有一个隐含的约束是，漏桶漏水的速度最好是一个整数值（即容量 N 能够整除时间窗口大小 T ），否则在计算剩余水量时会有些许误差。
4 令牌桶
漏桶模型中，请求来了是往桶里注水; 令牌桶的思想则完全相反，把请求放行变成从桶里抽水，对应的，把注水看作是补充系统可承受流量。
令牌桶算法的原理是系统以恒定的速率往桶里放入令牌，令牌桶有一个容量，当令牌桶满了，再向桶里放的令牌会被丢弃；当一个请求需要被处理，需要从令牌桶中取出一个令牌，如果此时令牌桶中没有令牌可取，那么拒绝该请求。
代码实现
class TokenBucket {
public:
TokenBucket(int64_t capacity, int64_t rate)
: capacity_(capacity),
rate_(rate),
supply_unit_time_(NS_PER_SECOND / rate) {}
// 尝试获取令牌
bool tryAcquire(int permits) {
int64_t cur = Now();
int64_t new_tokens = (cur - last_time_) / supply_unit_time_;
// 更新补充时间, 不能直接=cur, 否则会导致时间丢失
last_time_ += new_tokens * supply_unit_time_;
tokens_ = std::min(capacity_, tokens_ + new_tokens);
if (tokens_ >= permits) {
tokens_ -= permits;
return true;
} else {
return false;
}
}
private:
// 当前桶内的令牌数
int64_t tokens_ = 0;
// 上次补充令牌的时间(单位纳秒)
int64_t last_time_ = Now();
// 令牌桶大小
int64_t capacity_;
// 补充令牌的速率
int64_t rate_;
// 补充令牌的单位时间
const int64_t supply_unit_time_;
};
class TokenBucket {
public:
TokenBucket(int64_t capacity, int64_t rate)
: capacity_(capacity),
rate_(rate),
supply_unit_time_(NS_PER_SECOND / rate) {}
// 尝试获取令牌
bool tryAcquire(int permits) {
int64_t now = Now();
int64_t count = (now - last_time_) / supply_unit_time_;
int64_t new_tokens = count * supply_unit_time_ * rate_ / NS_PER_SECOND;
// 更新补充时间, 不能直接=now, 否则会导致时间丢失
last_time_ += count * supply_unit_time_;
tokens_ = std::min(capacity_, tokens_ + new_tokens);
if (tokens_ >= permits) {
tokens_ -= permits;
return true;
} else {
return false;
}
}
private:
// 当前桶内的令牌数
int64_t tokens_ = 0;
// 上次补充令牌的时间(单位纳秒)
int64_t last_time_ = Now();
// 令牌桶大小
int64_t capacity_;
// 补充令牌的速率
int64_t rate_;
// 补充令牌的单位时间
const int64_t supply_unit_time_ = NS_PER_US;
};
class DynamicTokenBucket {
double zeroTime_;
public:
explicit DynamicTokenBucket(double zeroTime = 0) noexcept
: zeroTime_(zeroTime) {}
bool tryAcquire(double permits, double rate, double burstSize,
int64_t now = Now()) {
double tokens = std::min((now / 1e9 - zeroTime_) * rate, burstSize);
if (tokens < permits) {
return false;
}
tokens -= permits;
zeroTime_ = now / 1e9 - tokens / rate;
return true;
}
};
class TokenBucket {
DynamicTokenBucket tokenBucket_;
double rate_;
double burstSize_;
public:
TokenBucket(double rate, double burstSize, double zeroTime = 0) noexcept
: tokenBucket_(zeroTime), rate_(rate), burstSize_(burstSize) {}
bool tryAcquire(double permits, int64_t now = Now()) {
return tokenBucket_.tryAcquire(permits, rate_, burstSize_, now);
}
};
漏桶、令牌桶的区别
虽然两者本质上只是反转了一下，不过在实际使用中，适用的场景稍有差别：
1）漏桶：用于控制网络中的速率。在该算法中，输入速率可以变化，但输出速率保持恒定。常常配合一个 FIFO 队列使用。
2）令牌桶：按照固定速率往桶中添加令牌，允许输出速率根据突发大小而变化。
举个例子，一个系统限制 60 秒内的最大访问量是 60 次，换算速率是 1 次/秒，如果在一段时间内没有访问量，那么对漏桶而言此刻是空的。现在，一瞬间涌入 60 个请求，那么流量整形后，漏桶会以每秒 1 个请求的速度，花上 1 分钟将 60 个请求漏给下游。换成令牌桶的话，则是从令牌桶中一次性取走 60 个令牌，一下子塞给下游。
5 滑动日志
一般情况下，上述的算法已经能很好地用于大部分实际应用场景了，很少有场景需要真正完全精确的控制（即任意给定时间窗口T内请求量不大于 N ）。如果要精确控制的话，我们需要记录每一次用户请求日志，当每次流控判断时，取出最近时间窗口内的日志数，看是否大于流控阈值。这就是滑动日志的算法思路。
设想某一个时刻 t 有一个请求，要判断是否允许，我们要看的其实是过去 t - N 时间段内是否有大于等于 N 个请求被放行，因此只要系统维护一个队列 q，里面记录每一个请求的时间，理论上就可以计算出从 t - N 时刻开始的请求数。
考虑到只需关心当前时间之前最长 T 时间内的记录，因此队列 q 的长度可以动态变化，并且队列中最多只记录 N 条访问，因此队列长度的最大值为 N。
滑动日志与滑动窗口非常像，区别在于滑动日志的滑动是根据日志记录的时间做动态滑动，而滑动窗口是根据子窗口的大小，以子窗口维度滑动。
伪代码实现
算法的伪代码表示如下：
# 初始化
counter = 0
q = []
# 请求处理流程
# 1.找到队列中第一个时间戳>=t-T的请求，即以当前时间t截止的时间窗口T内的最早请求
t = now
start = findWindowStart(q, t)
# 2.截断队列，只保留最近T时间窗口内的记录和计数值
q = q[start, q.length - 1]
counter -= start
# 3.判断是否放行，如果允许放行则将这次请求加到队列 q 的末尾
if counter < threshold
push(q, t)
counter++
# 放行
else
# 限流
findWindowStart 的实现依赖于队列 q 使用的数据结构，以简单的数组为例，可以使用二分查找等方式。后面也会看到使用其他数据结构如何实现。
如果用数组实现，一个难点可能是如何截断一个队列，一种可行的思路是使用一组头尾指针 head 和 tail 分别指向数组中最近和最早的有效记录索引来解决， findWindowStart 的实现就变成在 tail 和 head 之间查找对应元素。
复杂度问题
虽然算法解决了精确度问题，但代价也是显而易见的。
首先，我们要保存一个长度最大为 N 的队列，这意味着空间复杂度达到 O(N)，如果要针对不同的 key 做流控，那么空间上会占用更多。当然，可以对不活跃 key 的队列进行复用来降低内存消耗。
其次，我们需要在队列中确定时间窗口，即通过 findWindowStart 方法寻找不早于当前时间戳 t - N 的请求记录。以二分查找为例，时间复杂度是 O(logN)。
总结
这里按我的个人理解总结了上述几种流控算法的复杂度和适用场景。
| 算法 | 时间复杂度 | 空间复杂度 | 适用场景 |
|---|---|---|---|
| 固定窗口 | O(1) | O(1) | 容易实现,适用于一些简单的流控场景,流量比较均匀,或者允许临界突变 |
| 滑动窗口 | O(1) | O(M) - M为子窗口数 | 适用大多数场景,可以通过调节采样子窗口数来平衡开销 |
| 漏桶算法 | O(1) | O(1) | 要求输出速率恒定的场景,能够平滑流量 |
| 令牌桶算法 | O(1) | O(1) | 与漏桶类似,区别在于允许一定的突发流量 |
| 滑动日志 | O(log(N)) 取决于选择的数据结构 | O(N) - N为时间窗口内允许的最大请求量 | 要求完全精确的控制,保证任意T时刻内流量不超过N,高时间和高空间复杂度,性能最差 |
完整代码
#include <chrono>
#include <cstdint>
#include <cstdio>
#include <ctime>
#include <thread>
const int NS_PER_SECOND = 1e9;
const int NS_PER_MS = 1e6;
const int NS_PER_US = 1e3;
// 获取当前时间戳, 单位纳秒
int64_t Now() {
struct timespec ts;
clock_gettime(CLOCK_MONOTONIC, &ts);
return ts.tv_sec * NS_PER_SECOND + ts.tv_nsec;
}
class RateLimiter {
// 时间窗口, 单位秒
int64_t window_;
// 时间窗口内最大允许的阈值
int64_t threshold_;
// 当前时间窗口的起始时间
int64_t start_time_ = Now();
// 计数器
int64_t counter_;
public:
RateLimiter(int64_t window, int64_t threshold)
: window_(window), threshold_(threshold) {}
bool tryAcquire(int permits) {
long now = Now();
if (now - start_time_ > window_ * NS_PER_SECOND) {
counter_ = 0;
start_time_ = now;
}
if (counter_ + permits <= threshold_) {
counter_ += permits;
return true;
} else {
return false;
}
}
};
class LeakyBucket {
int64_t last_time_ = Now();
int64_t rate_;
int64_t debt_;
// 精度
int64_t precision_;
int64_t quota_;
public:
LeakyBucket(int64_t rate, double precision = 1000)
: rate_(rate), precision_(precision) {
quota_ = rate_ / precision_;
}
bool tryAcquire(int permits) {
int64_t now = Now();
int count = (now - last_time_) / (NS_PER_SECOND / precision_);
int64_t pay_off = count * quota_;
int64_t left_debt = std::max(0LL, debt_ - pay_off);
if (left_debt > quota_) {
return false;
}
debt_ = left_debt + permits;
last_time_ += count * (NS_PER_SECOND / precision_);
return true;
}
};
class TokenBucket {
public:
TokenBucket(int64_t capacity, int64_t rate)
: capacity_(capacity),
rate_(rate),
supply_unit_time_(NS_PER_SECOND / rate) {}
// 尝试获取令牌
bool tryAcquire(int permits) {
int64_t now = Now();
int64_t count = (now - last_time_) / supply_unit_time_;
int64_t new_tokens = count * supply_unit_time_ * rate_ / NS_PER_SECOND;
// 更新补充时间, 不能直接=now, 否则会导致时间丢失
last_time_ += count * supply_unit_time_;
tokens_ = std::min(capacity_, tokens_ + new_tokens);
if (tokens_ >= permits) {
tokens_ -= permits;
return true;
} else {
return false;
}
}
private:
// 当前桶内的令牌数
int64_t tokens_ = 0;
// 上次补充令牌的时间(单位纳秒)
int64_t last_time_ = Now();
// 令牌桶大小
int64_t capacity_;
// 补充令牌的速率
int64_t rate_;
// 补充令牌的单位时间
const int64_t supply_unit_time_ = NS_PER_US;
};
int main() {
// 限流300MB/s
// RateLimiter limiter(1, 300 * 1024 * 1024);
// LeakyBucket limiter(300 * 1024 * 1024);
TokenBucket limiter(1024 * 1024, 300 * 1024 * 1024);
// 每次请求256KB
int64_t request_size = 256 * 1024;
// 每隔约1ms发起2次请求
// 每隔1s打印一次请求数据量
int64_t start_time = Now();
int64_t last_time = start_time;
int64_t last_size = 0;
while (true) {
int64_t now = Now();
if (now - last_time >= NS_PER_SECOND) {
printf("time: %lf s, request size: %lf MB\n", (now - last_time) / 1e9,
(last_size / 1024.0 / 1024.0));
last_time = now;
last_size = 0;
}
for (int i = 0; i < 2; ++i) {
if (limiter.tryAcquire(request_size)) {
last_size += request_size;
}
}
std::this_thread::sleep_for(std::chrono::milliseconds(1));
}
return 0;
}到此这篇关于一文带你搞懂C++中的流量控制的文章就介绍到这了,更多相关C++流量控制内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！
相关文章
当程序与外界进行信息交换时，存在两个对象，一个是程序中的对象，另一个是文件对象。流是信息流动的一种抽象，它负责在数据的生产者和数据的消费者之间建立联系，并管理数据的流动2022-07-07
这篇文章主要为大家详细介绍了C++ vector容器的使用，文中示例代码介绍的非常详细，具有一定的参考价值，感兴趣的小伙伴们可以参考一下，希望能够给你带来帮助2022-03-03
list相较于vector来说会显得复杂,它的好处是在任意位置插入,删除都是一个O(1)的时间复杂度,本文主要介绍了C++中List的模拟实现，文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值，需要的朋友们下面随着小编来一起学习学习吧2022-07-07
这篇文章主要介绍了C语言双向链表的表示与实现，对于研究数据结构域算法的朋友有一定的参考借鉴价值,需要的朋友可以参考下2014-07-07
本篇文章是对在C语言中局部变量与全局变量在内存中的存放位置进行了详细的分析介绍，需要的朋友参考下2013-05-05
多态是指同样的消息被不同的对象接收时导致不同的行为。本文通过实例代码给大家介绍了C++多态性与虚函数的相关知识，感兴趣的朋友一起看看吧2020-02-02
这篇文章主要介绍了C++ string替换单个指定字符为其它字符问题，具有很好的参考价值，希望对大家有所帮助。如有错误或未考虑完全的地方，望不吝赐教2023-06-06
这篇文章主要介绍了Qt QChart 创建图表的实现方法，文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值，需要的朋友们下面随着小编来一起学习学习吧2020-12-12
最近在研究C++的各种编译构建过程，学习了一下cmake，gyp/ninja这些自动化构建工具后，想着自己试下用纯命令行跑一遍编译流程。在试图把C++静态库编译为动态库的过程中遇到了棘手的问题，找了好久后发现是跟Mac平台相关的，这里记录一下，望对遇到类似问题的童鞋有帮助。2016-12-12
这篇文章主要介绍了C语言利用链表与文件实现登录注册功能，文中示例代码介绍的非常详细，具有一定的参考价值，感兴趣的小伙伴们可以参考一下2020-12-12
最新评论