Java的非对称加密(RSA、数字签名、数字证书)详解
1. 什么是非对称加密
(1)公钥和私钥成对出现
(2)公钥加密、私钥解密,私钥加密、公钥解密
(3)公钥一般对外公开,私钥保密
(4)主要用于防止通信数据被篡改,保证数据的完整性,也可对明文来实现保密
对称加密:加密和解密使用同一个密钥
非对称加密:加密、解密使用不同的两把密钥,这两把密钥成对
一般通信开始时通过非对称加密将对称加密的密钥发送给另一方,然后双方通过对称加密来进行沟通
2. 常用的非对称加密算法
常用的非对称加密算法有:RSA、ECC 对比:
(1) RSA签名算法适合于:Verify操作频度高,而Sign操作频度低的应用场景。
比如,分布式系统中基于capability的访问控制就是这样的一种场景。
(2) ECC签名算法适合于:Sign和Verify操作频度相当的应用场景。
比如,点对点的安全信道建立。【移动互联网用的比较多】
3. 数字签名(digital signature)
数字签名: 数字签名由数字摘要和非对称加密技术组成
(1)明文数据通过摘要算法得到固定长度的摘要信息
(2)用私钥加密摘要信息即可得到数字签名,将明文数据和签名发送到另一方
(3)另一方用公钥解密签名后得到摘要信息,摘要算法提取明文的摘要信息后与解密的摘要信息进行比对,如果相同则证明明文数据完整,未被篡改
4. 数字证书(digital certificate)
(1)证书认证中心(certificate authority,简称CA )用私钥加密被认证网站的公钥和其他网站信息(如网址),生成数字证书,网站用公钥加密明文数据后,附带数字证书,发送给访问方【客户端】。
(2)本地客户端(浏览器)的"证书管理器",有"受信任的根证书颁发机构"列表。客户端会根据这张列表,查看解开数字证书的公钥。客户端使用CA的公钥解密数字证书后获取到网站的公钥,再用公钥解密数据,获取明文
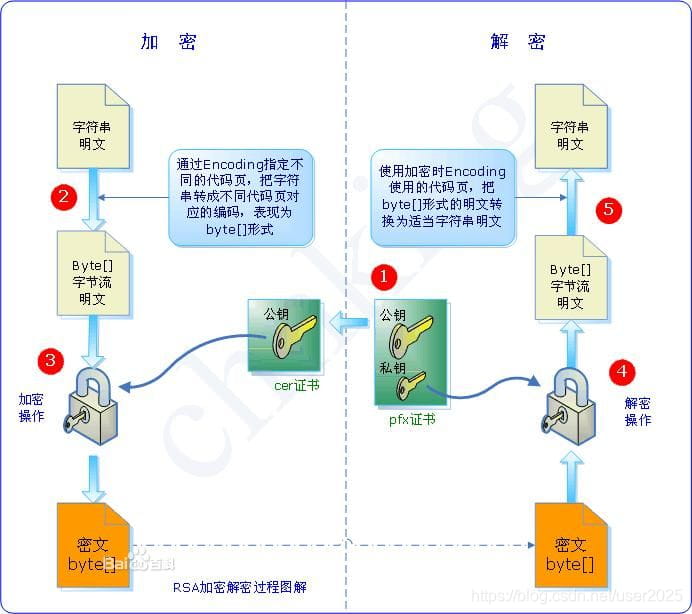
5. java实现RSA加解密
import org.apache.tomcat.util.codec.binary.Base64;
import javax.crypto.Cipher;
import java.nio.charset.StandardCharsets;
import java.security.KeyFactory;
import java.security.KeyPair;
import java.security.KeyPairGenerator;
import java.security.NoSuchAlgorithmException;
import java.security.SecureRandom;
import java.security.interfaces.RSAPrivateKey;
import java.security.interfaces.RSAPublicKey;
import java.security.spec.PKCS8EncodedKeySpec;
import java.security.spec.X509EncodedKeySpec;
import java.util.HashMap;
import java.util.Map;
public class RSAEncrypt {
//用于封装随机产生的公钥与私钥
private static Map<Integer, String> keyMap = new HashMap<Integer, String>();
public static void main(String[] args) throws Exception {
//生成公钥和私钥
genKeyPair();
//加密字符串
String message = "123456";
System.out.println("随机生成的公钥为:" + keyMap.get(0));
System.out.println("随机生成的私钥为:" + keyMap.get(1));
String messageEn = encrypt(message, keyMap.get(0));
System.out.println(message + "\t加密后的字符串为:" + messageEn);
String messageDe = decrypt(messageEn, keyMap.get(1));
System.out.println("还原后的字符串为:" + messageDe);
}
/**
* 随机生成密钥对
*
* @throws NoSuchAlgorithmException
*/
public static void genKeyPair() throws NoSuchAlgorithmException {
// KeyPairGenerator类用于生成公钥和私钥对,基于RSA算法生成对象
KeyPairGenerator keyPairGen = KeyPairGenerator.getInstance("RSA");
// 初始化密钥对生成器,密钥大小为96-1024位
keyPairGen.initialize(1024, new SecureRandom());
// 生成一个密钥对,保存在keyPair中
KeyPair keyPair = keyPairGen.generateKeyPair();
// 得到私钥
RSAPrivateKey privateKey = (RSAPrivateKey) keyPair.getPrivate();
// 得到公钥
RSAPublicKey publicKey = (RSAPublicKey) keyPair.getPublic();
//得到公钥字符串
String publicKeyString = new String(Base64.encodeBase64(publicKey.getEncoded()), StandardCharsets.UTF_8);
// 得到私钥字符串
String privateKeyString = new String(Base64.encodeBase64((privateKey.getEncoded())), StandardCharsets.UTF_8);
// 将公钥和私钥保存到Map
keyMap.put(0, publicKeyString); //0表示公钥
keyMap.put(1, privateKeyString); //1表示私钥
}
/**
* RSA公钥加密
*
* @param str 加密字符串
* @param publicKey 公钥
* @return 密文
* @throws Exception 加密过程中的异常信息
*/
public static String encrypt(String str, String publicKey) throws Exception {
//base64编码的公钥
byte[] decoded = Base64.decodeBase64(publicKey);
RSAPublicKey pubKey = (RSAPublicKey) KeyFactory.getInstance("RSA").generatePublic(new X509EncodedKeySpec(decoded));
//RSA加密
Cipher cipher = Cipher.getInstance("RSA");
cipher.init(Cipher.ENCRYPT_MODE, pubKey);
return Base64.encodeBase64String(cipher.doFinal(str.getBytes(StandardCharsets.UTF_8)));
}
/**
* RSA私钥解密
*
* @param str 加密字符串
* @param privateKey 私钥
* @return 铭文
* @throws Exception 解密过程中的异常信息
*/
public static String decrypt(String str, String privateKey) throws Exception {
//64位解码加密后的字符串
byte[] inputByte = Base64.decodeBase64(str.getBytes(StandardCharsets.UTF_8));
//base64编码的私钥
byte[] decoded = Base64.decodeBase64(privateKey);
RSAPrivateKey priKey = (RSAPrivateKey) KeyFactory.getInstance("RSA").generatePrivate(new PKCS8EncodedKeySpec(decoded));
//RSA解密
Cipher cipher = Cipher.getInstance("RSA");
cipher.init(Cipher.DECRYPT_MODE, priKey);
return new String(cipher.doFinal(inputByte));
}
}到此这篇关于Java的非对称加密(RSA、数字签名、数字证书)详解的文章就介绍到这了,更多相关Java的非对称加密内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
相关文章

浅谈SpringCloud feign的http请求组件优化方案
这篇文章主要介绍了浅谈SpringCloud feign的http请求组件优化方案,具有很好的参考价值,希望对大家有所帮助。一起跟随小编过来看看吧2021-02-02












最新评论