Java中如何编写一个数的n次方（幂运算）?

更新时间：2024年07月13日 15:14:30 作者：拼搏@

本文介绍了使用pow函数和自定义for循环计算幂的O(n)时间复杂度方法,然后重点讲解了快速幂算法的分治思想,以及从二进制角度的解释,包括如何通过位运算和循环迭代实现高效计算,给出了Java代码实现

一、算法简介

1.使用pow函数和自定义的for循环的时间复杂度为O(n)

/**计算x的y次方**/
//1.使用Pow函数
double res = Math.pow(x,y);
//2.自定义for循环
double res=x;
for(int i=1;i<y;i++){
     res=res*x;
}

2.快速幂的时间复杂度为O(log n)

二、快速幂的思想

（1）从分冶的角度出发，计算 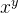$x^{y}$

①假设y为偶数，即计算 $3^{8}$

$3^{8}=3^{2*4}=9^{4}=9^{2*2}=81^{2}$ = $6561^{1}$

我们将指数 y,每次划分为 $\frac{y}{2}$ ,上述式子不需要进行8次循环，而只需要三步即可完成，注 $3^{2*4}$ 和 $9^{2*2}$ 是为了让读者好理解，而重复写的。

②假设y为奇数，即计算 $3^{11}$

$3^{11}=3^{1+10}=3*3^{10}=3*9^{5}=3*9^{1+4}=3*9*81^{2}$ = $3*9*6561^{1}$

指数部分为奇数是可以化解成（1+偶数）的形式的，这样我们可以把指数为1的底拿出来当答案来乘，偶数部分同①继续化解即可

伪代码
    x=3,y=10,res=1
   while(指数y不等于0){
    if(指数y为奇数){
        res = res * x //提取底数出来，作为乘积
    }
    y=y/2 //指数二分
    x=x*x //底数平方

}

(2) 从二进制的角度出发

如8的二进制位：8= $1000_{2}$ ；

二进制转十进制： $1000_{2}$ = $1*2^3+0*2^2+0*2^1+0*2^0$ =8

那么 $3^8=3^{(1000)_{2}}$ = $3^{1*2^3+0*2^2+0*2^1+0*2^0}$ = $3^{0*2^0}*3^{0*2^1}*3^{0*2^2}*3^{1*2^3}$ (倒序写)

观察发现：指数部分是由两部分组成，第一部分是0001，第二部分是 $2^0,2^1,2^2,2^3$ ，发现2是循环增大的（用代码x=x*x,循环迭代出来，但是否使用则看二进制位是否为‘1’），由于二进制要么为0要么为1（用代码 y&1==1,来判断）

再举个详细的例子(计算 $3^{11}$ )：

11=1011

$3^{11}=3^{1*2^{0}}*3^{1*2^{1}}*3^{0*2^{2}}*3^{1*2^{3}}$ = $3^{1*1}*3^{1*2}*3^{0*4}*3^{1*8}$

伪代码：

 x=3,y=11,res=1

 while( （1011）y从尾往头读取){

  if( (y&1)==1){

     res=res*x;  //二进制位不为0，则相乘

     //如第一个1：res=1*3,    

     //第二个1：res=res*3^2

     //第三个数为0：不相乘，但x是不断平方的，此时是x^4

     //第四个数为1：res=res*3^8  ,注意哦，平方是在if后面

       }

    二进制右移一位

    x=x*x; //依次迭代3^0,3^1,3^2，3^4,3^8................

 }

三、代码实现

   public static double FastPow(int x,int y){
        double res= 1;
        while (y!=0){ 
            if(y%2 == 1){ //指数为奇数，也可以利用位运算：(y&1)==1 （与操作）： 判断 n 二进制最右一位是否为 1
                res *= x;
            }
            y=y/2;  //指数循环二分,y>>=1 （移位操作）： n 右移一位（可理解为删除最后一位,即除以2）。
            x=x*x;  //底数平分

        }
        return res;
    }

到此这篇关于Java中如何编写一个数的n次方（幂运算）?的文章就介绍到这了,更多相关Java中的幂运算(幂函数)内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！

如何解决@value获取不到yaml数组的问题
文章介绍了在使用YAML配置文件时,通过@Value注解获取整数和数组列表的配置方法,并提供了两种解决方案：一种适用于非嵌套列表,另一种适用于嵌套列表等复杂配置
2024-11-11
SpringBoot3.2.2整合MyBatis Plus3.5.5的详细过程
这篇文章给大家介绍了SpringBoot3.2.2整合MyBatis Plus3.5.5的详细过程,文中通过代码示例给大家介绍的非常详细,对大家的学习或工作有一定的帮助,需要的朋友可以参考下
2024-01-01
Java多线程通信实现方式详解
这篇文章主要介绍了Java多线程通信实现方式详解,文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下
2019-11-11
关于Spring中声明式事务的使用详解
Spring中事务分为编程式事务和声明式事务,编程式事务由于需要在代码中硬编码,在实际项目开发中比较少用到,实际开发中用的比较多的就是声明式事务,这篇文章主要给大家介绍了关于Spring中声明式事务使用的相关资料,需要的朋友可以参考下
2021-08-08
java集合Collection常用方法解读
这篇文章主要介绍了java集合Collection常用方法解读，具有很好的参考价值，希望对大家有所帮助。如有错误或未考虑完全的地方，望不吝赐教
2023-03-03
java 商户PC端接入支付宝支付的实现方法
这篇文章主要介绍了java 商户PC端接入支付宝支付的实现方法，文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值，需要的朋友们下面随着小编来一起学习学习吧
2019-08-08
SpringBoot如何获取application.properties中自定义的值
这篇文章主要介绍了SpringBoot获取application.properties中的自定义的值,目录结构文件代码给大家列举的非常详细，需要的朋友可以参考下
2021-09-09
SpringBoot资源文件的存放位置设置方式
这篇文章主要介绍了SpringBoot资源文件的存放位置设置方式，具有很好的参考价值，希望对大家有所帮助。如有错误或未考虑完全的地方，望不吝赐教
2021-11-11
Java static方法用法实战案例总结
这篇文章主要介绍了Java static方法用法,结合具体案例形式总结分析了java static方法功能、使用方法及相关操作注意事项,需要的朋友可以参考下
2019-09-09
IDEA与MyEclipse代码量统计方式
文章介绍在项目中不安装第三方工具统计代码行数的方法,分别说明MyEclipse通过正则搜索（排除空行和注释）及IDEA使用Statistic插件或调整搜索设置（修改ide.usages.page.size）的两种操作方式,并强调需根据需求灵活选择
2025-08-08